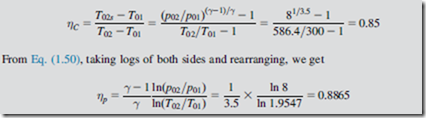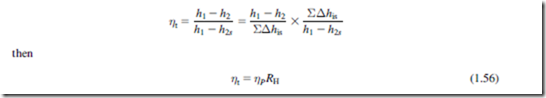Introduction, Basic Principles:Small stage or poly tropic efficiency

Small stage or polytropic efficiency

The isentropic efficiency described in the preceding section, although fundamentally valid, can be misleading if used for comparing the efficiencies of turbomachines of differing pressure ratios. Now, any turbomachine may be regarded as being composed of a large number of very small stages, irrespective of the actual number of stages in the machine. If each small stage has the same efficiency, then the isentropic efficiency of the whole machine will be different from the small stage efficiency, the difference depending upon the pressure ratio of the machine. This perhaps rather surprising result is a manifestation of a simple thermodynamic effect concealed in the expression for isentropic efficiency and is made apparent in the following argument.

Compression process

Figure 1.11 shows an enthalpy-entropy diagram on which adiabatic compression between pressures p1 and p2 is represented by the change of state between points 1 and 2. The corresponding reversible process is represented by the isentropic line 1 to 2s. It is assumed that the compression process may be divided into a large number of small stages of equal efficiency ηp. For each small stage the actual work input is δW and the corresponding ideal work in the isentropic process is δWmin. With the notation of Figure 1.11,

Since each small stage has the same efficiency, then ηp 5 ðΣδWmin=ΣδWÞ is also true.

From the relation Tds 5 dh 2 vdp, for a constant pressure process, (@h/@s)p1 5 T. This means that the higher the fluid temperature, the greater is the slope of the constant pressure lines on the Mollier diagram. For a gas where h is a function of T, constant pressure lines diverge and the slope of the line p2 is greater than the slope of line p1 at the same value of entropy. At equal values of T, constant pressure lines are of equal slope as indicated in Figure 1.11. For the special case of a perfect gas (where Cp is constant), Cp(dT/ds) 5 T for a constant pressure process. Integrating this expression results in the equation for a constant pressure line, s 5 CplogT 1 constant.

Returning now to the more general case, since

Thus, for a compression process the isentropic efficiency of the machine is less than the small stage efficiency, the difference being dependent upon the divergence of the constant pressure lines. Although the foregoing discussion has been in terms of static states it also applies to stagnation states since these are related to the static states via isentropic processes.

Small stage efficiency for a perfect gas

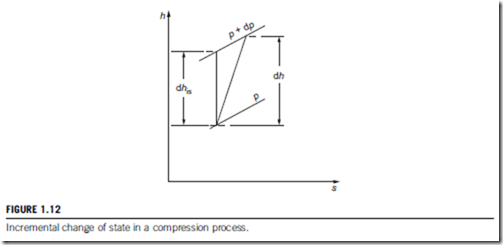
An explicit relation can be readily derived for a perfect gas between small stage efficiency, the overall isentropic efficiency and the pressure ratio. The analysis is for the limiting case of an infinitesimal compressor stage in which the incremental change in pressure is dp as indicated in Figure 1.12. For the actual process the incremental enthalpy rise is dh and the corresponding ideal enthalpy rise is dhis.

The polytropic efficiency for the small stage is

Values of “overall” isentropic efficiency have been calculated using Eq. (1.53) for a range of pressure ratio and different values of ηp; these are plotted in Figure 1.13. This figure amplifies the observation made earlier that the isentropic efficiency of a finite compression process is less than the efficiency of the small stages. Comparison of the isentropic efficiency of two machines of different pressure ratios is not a valid procedure since, for equal polytropic efficiency, the compressor with the higher pressure ratio is penalized by the hidden thermodynamic effect.

EXAMPLE 1.6

An axial flow air compressor is designed to provide an overall total-to-total pressure ratio of 8 to 1. At inlet and outlet the stagnation temperatures are 300 and 586.4 K, respectively.

Determine the overall total-to-total efficiency and the polytropic efficiency for the compres- sor. Assume that γ for air is 1.4.

Solution

From Eq. (1.46), substituting h 5 CpT, the efficiency can be written as

Turbine polytropic efficiency

A similar analysis to the compression process can be applied to a perfect gas expanding through an adiabatic turbine. For the turbine the appropriate expressions for an expansion, from a state 1 to a state 2, are

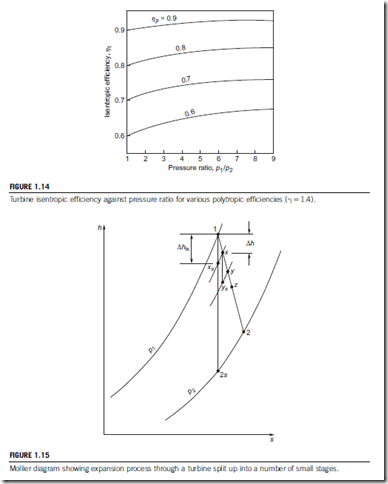
The derivation of these expressions is left as an exercise for the student. “Overall” isentropic efficiencies have been calculated for a range of pressure ratios and polytropic efficiencies, and these are shown in Figure 1.14. The most notable feature of these results is that, in contrast with a compression process, for an expansion, isentropic efficiency exceeds small stage efficiency.

Reheat factor

The foregoing relations cannot be applied to steam turbines as vapors do not obey the perfect gas laws. It is customary in steam turbine practice to use a reheat factor RH as a measure of the inefficiency of the complete expansion. Referring to Figure 1.15, the expansion process through an

adiabatic turbine from state 1 to state 2 is shown on a Mollier diagram, split into a number of small stages. The reheat factor is defined as

Due to the gradual divergence of the constant pressure lines on a Mollier chart, RH is always greater than unity. The actual value of RH for a large number of stages will depend upon the position of the expansion line on the Mollier chart and the overall pressure ratio of the expansion. In normal steam turbine practice the value of RH is usually between 1.03 and 1.08.

Now, since the isentropic efficiency of the turbine is