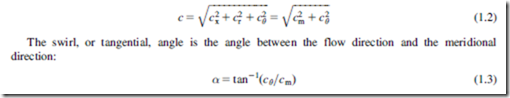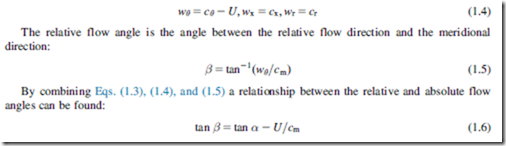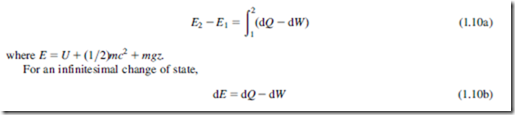Introduction, Basic Principles:Definition of a turbomachine and Coordinate system

Introduction, Basic Principles

Definition of a turbomachine

We classify as turbomachines all those devices in which energy is transferred either to, or from, a continuously flowing fluid by the dynamic action of one or more moving blade rows. The word turbo or turbinis is of Latin origin and implies that which spins or whirls around. Essentially, a rotating blade row, a rotor or an impeller changes the stagnation enthalpy of the fluid moving through it by doing either positive or negative work, depending upon the effect required of the machine. These enthalpy changes are intimately linked with the pressure changes occurring simultaneously in the fluid.

Two main categories of turbomachine are identified: first, those that absorb power to increase the fluid pressure or head (ducted and unducted fans, compressors, and pumps); second, those that produce power by expanding fluid to a lower pressure or head (wind, hydraulic, steam, and gas tur- bines). Figure 1.1 shows, in a simple diagrammatic form, a selection of the many varieties of turbo- machines encountered in practice. The reason that so many different types of either pump (compressor) or turbine are in use is because of the almost infinite range of service requirements. Generally speaking, for a given set of operating requirements one type of pump or turbine is best suited to provide optimum conditions of operation.

Turbomachines are further categorized according to the nature of the flow path through the pas- sages of the rotor. When the path of the through-flow is wholly or mainly parallel to the axis of rotation, the device is termed an axial flow turbomachine (e.g., Figures 1.1(a) and (e)). When the path of the through-flow is wholly or mainly in a plane perpendicular to the rotation axis, the device is termed a radial flow turbomachine (e.g., Figure 1.1(c)). More detailed sketches of radial flow machines are given in Figures 7.3, 7.4, 8.2, and 8.3. Mixed flow turbomachines are widely used. The term mixed flow in this context refers to the direction of the through-flow at the rotor outlet when both radial and axial velocity components are present in significant amounts. Figure 1.1(b) shows a mixed flow pump and Figure 1.1(d) a mixed flow hydraulic turbine.

One further category should be mentioned. All turbomachines can be classified as either impulse or reaction machines according to whether pressure changes are absent or present, respectively, in the flow through the rotor. In an impulse machine all the pressure change takes place in one or more nozzles, the fluid being directed onto the rotor. The Pelton wheel, Figure 1.1(f), is an example of an impulse turbine.

The main purpose of this book is to examine, through the laws of fluid mechanics and thermo- dynamics, the means by which the energy transfer is achieved in the chief types of turbomachines, together with the differing behavior of individual types in operation. Methods of analyzing the flow processes differ depending upon the geometrical configuration of the machine, whether the fluid can be regarded as incompressible or not, and whether the machine absorbs or produces work. As far as possible, a unified treatment is adopted so that machines having similar configurations and function are considered together.

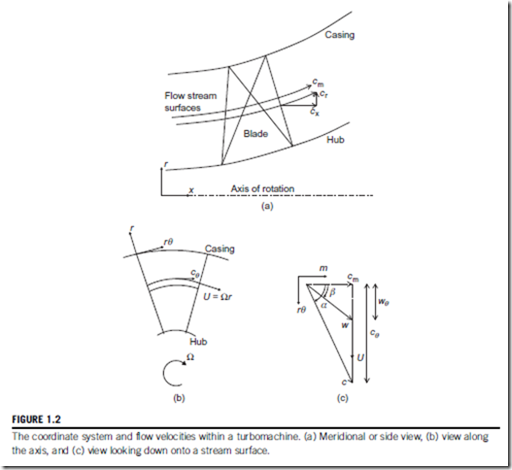
Coordinate system

Turbomachines consist of rotating and stationary blades arranged around a common axis, which means that they tend to have some form of cylindrical shape. It is therefore natural to use a

cylindrical polar coordinate system aligned with the axis of rotation for their description and analysis. This coordinate system is pictured in Figure 1.2. The three axes are referred to as axial x, radial r, and tangential (or circumferential) rθ.

In general, the flow in a turbomachine has components of velocity along all three axes, which vary in all directions. However, to simplify the analysis it is usually assumed that the flow does not vary in the tangential direction. In this case, the flow moves through the machine on axi-symmetric stream surfaces, as drawn on Figure 1.2(a). The component of velocity along an axi-symmetric stream surface is called the meridional velocity,

In purely axial flow machines the radius of the flow path is constant and, therefore, referring to Figure 1.2(c) the radial flow velocity will be zero and cm 5 cx. Similarly, in purely radial flow machines the axial flow velocity will be zero and cm 5 cr. Examples of both of these types of machines can be found in Figure 1.1.

The total flow velocity is made up of the meridional and tangential components and can be written

Relative velocities

The analysis of the flow-field within the rotating blades of a turbomachine is performed in a frame of reference that is stationary relative to the blades. In this frame of reference the flow appears as steady, whereas in the absolute frame of reference it would be unsteady. This makes any calculations significantly easier, and therefore the use of relative velocities and relative flow quantities is fundamental to the study of turbomachinery.

The relative velocity w is the vector subtraction of the local velocity of the blade U from the absolute velocity of the flow c, as shown in Figure 1.2(c). The blade has velocity only in the tangential direction, and therefore the components of the relative velocity can be written as

Sign convention

Equations (1.4) and (1.6) suggest that negative values of flow angles and velocities are possible. In many turbomachinery courses and texts, the convention is to use positive values for tangential velocities that are in the direction of rotation (as they are in Figure 1.2(b) and (c)), and negative values for tangential velocities that are opposite to the direction of rotation. The convention adopted in this book is to ensure that the correct vector relationship between the relative and abso- lute velocities is applied using only positive values for flow velocities and flow angles.

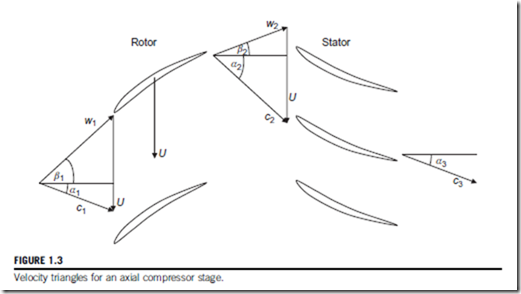
Velocity diagrams for an axial flow compressor stage

A typical stage of an axial flow compressor is shown schematically in Figure 1.3 (looking radially inwards) to show the arrangement of the blading and the flow onto the blades.

The flow enters the stage at an angle α1 with a velocity c1. This inlet velocity is set by whatever is directly upstream of the compressor stage: an inlet duct, another compressor stage or an inlet guide vane (IGV). By vector subtraction the relative velocity entering the rotor will have a magnitude w1 at a relative flow angle β1. The rotor blades are designed to smoothly accept this relative flow and change its direction so that at outlet the flow leaves the rotor with a relative velocity w2 at a relative flow angle β2. As shown later in this chapter, work will be done by the rotor blades on the gas during this process and, as a consequence, the gas stagnation pressure and stagnation temperature will be increased.

By vector addition the absolute velocity at rotor exit c2 is found at flow angle α2. This flow should smoothly enter the stator row which it then leaves at a reduced velocity c3 at an absolute angle α3. The diffusion in velocity from c2 to c3 causes the pressure and temperature to rise further. Following this the gas is directed to the following rotor and the process goes on repeating through the remaining stages of the compressor.

The purpose of this brief explanation is to introduce the reader to the basic fluid mechanical processes of turbomachinery via an axial flow compressor. It is hoped that the reader will follow the description given in relation to the velocity changes shown in Figure 1.3 as this is fundamental to understanding the subject of turbomachinery. Velocity triangles will be considered in further detail for each category of turbomachine in later chapters.

EXAMPLE 1.1

The axial velocity through an axial flow fan is constant and equal to 30 m/s. With the notation given in Figure 1.3, the flow angles for the stage are α1 and β2 are 23o and β1 and α2 are 60o.

From this information determine the blade speed U and, if the mean radius of the fan is

0.15 m, find the rotational speed of the rotor.

Solution

The velocity components are easily calculated as follows:

The fundamental laws

The remainder of this chapter summarizes the basic physical laws of fluid mechanics and thermo- dynamics, developing them into a form suitable for the study of turbomachines. Following this, the properties of fluids, compressible flow relations and the efficiency of compression and expansion flow processes are covered.

The laws discussed are

i. the continuity of flow equation;

ii. the first law of thermodynamics and the steady flow energy equation;

iii. the momentum equation;

iv. the second law of thermodynamics.

All of these laws are usually covered in first-year university engineering and technology courses, so only the briefest discussion and analysis is given here. Some textbooks dealing comprehensively with these laws are those written by C¸ engel and Boles (1994), Douglas, Gasiorek and Swaffield (1995), Rogers and Mayhew (1992), and Reynolds and Perkins (1977). It is worth remembering that these laws are completely general; they are independent of the nature of the fluid or whether the fluid is compressible or incompressible.

The equation of continuity

Consider the flow of a fluid with density ρ, through the element of area dA, during the time interval dt. Referring to Figure 1.4, if c is the stream velocity the elementary mass is dm 5 ρcdtdA cosθ, where θ is the angle subtended by the normal of the area element to the stream direction.

The first law of thermodynamics

The first law of thermodynamics states that, if a system is taken through a complete cycle during which heat is supplied and work is done, then

where H dQ represents the heat supplied to the system during the cycle and H dW the work done by the system during the cycle. The units of heat and work in Eq. (1.9) are taken to be the same.

During a change from state 1 to state 2, there is a change in the energy within the system:

The steady flow energy equation

Many textbooks, e.g., C¸ engel and Boles (1994), demonstrate how the first law of thermodynamics is applied to the steady flow of fluid through a control volume so that the steady flow energy equation is obtained. It is unprofitable to reproduce this proof here and only the final result is quoted. Figure 1.5 shows a control volume representing a turbomachine, through which fluid passes at a steady rate of mass flow m_ , entering at position 1 and leaving at position 2. Energy is transferred from the fluid to the blades of the turbomachine, positive work being done (via the shaft) at the rate W_ x. In the general case positive heat transfer takes place at the rate Q_, from the surroundings to the control volume. Thus, with this sign convention the steady flow energy equation is