First Law & Thermodynamic Change
The First Law of Thermodynamics can be regarded as the macroscopic version of the conservation of energy law of physics. From the start, however, you are advised to keep the following Helpful Hint in mind.
System & Surroundings
As discussed in Section 5.1, the molecular state energy E is conserved (constant over time) if the system is isolated. An isolated system is one that has neither mechanical nor thermal contact with its surroundings—it might as well be “alone in the universe.”
Of course, this is not a very realistic picture. Generally speaking, con- tact between system and surroundings allows for changes not only of the
molecular state of the system (as in Section 5.1), but also its thermodynamic state—and that of the surroundings as well.
It can be convenient to consider the surroundings explicitly, as in Fig- ure 7.1. Treated as its own system, the surroundings has its own thermo- dynamic variables and quantities, denoted with a ‘sur’ subscript. Together, the system plus surroundings form the total system, whose quantities adopt a ‘tot’ subscript.
The picture above resembles the subsystems picture of Section 4.3, but with some key differences. Whereas subsystems are usually treated “equally,” the system and its surroundings are not. For instance, the surroundings are usually much larger than the system, as in the case of a heat bath (see Section 9.1).
Another difference is the requirement that the total system must be iso- lated. Arguments that apply only to isolated systems (such as energy con- servation) may then be referred to the total system—allowing the system itself to be more general. Of course, the precise division into “system” and “surroundings” is flexible.
⊳⊳⊳ Helpful Hint: As with independent variables, you are free to choose the “system” and “surroundings” for a given thermodynamics problem however you wish. Choose wisely—i.e., so as to make the problem easier to solve—and remain consistent in your choice from start to finish.
Thermodynamic Change
If “nothing ever happened” (see Talking Heads excerpt on p. 9), life would be pretty boring. This is the case with thermodynamic systems in equilibrium, so long as there is no change in external factors (Definition 4.1, p. 26). What happens when external factors do change? In most cases, this gives rise to a change of thermodynamic state. One obvious consequence of such a change is that at least one of the two independent variables must change its value.
We will often refer to the initial thermodynamic state as “state A,” and denote the initial values of thermodynamic quantities with an ‘i’ subscript. Likewise, “state B,” and ‘f ’ subscripts, are used for the final state. The change in the value of a generic quantity X , under the thermodynamic change, is then given as
ΔX = (Xf − Xi ). (7.1)
Note that most thermodynamic quantities—not just the variables—may be expected to change their values under a thermodynamic change. The surroundings quantities also undergo their own change.
One of the major reasons why thermodynamic processes can be so complicated is that there are two independent variables, rather than only one. Consequently, it is never sufficient to rely on a single variable only. An unambiguous description of a thermodynamic change requires a specification of what both independent variables are doing. That said, thermodynamic changes often occur under the special condition that one of the variables is held fixed (constant).
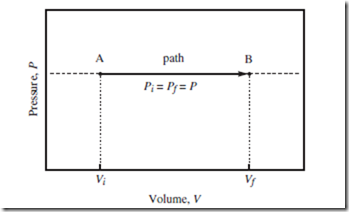
Thermodynamic changes can be represented using indicator diagrams— two-dimensional plots, in which each axis represents a different independent variable, and each point a different thermodynamic state. Indicator diagrams are often used to show the path taken through “state space,” to get from A to B, as in Figure 7.2.
First Law
In its most fundamental form above, the First Law is a statement about the total system. In order to convert Equation (7.2) into its more familiar, system-based form, we must consider the ways in which thermodynamic energy can be transferred between system and surroundings. As introduced in Section 4.3 (and to be further elaborated on in Section 8.2): mechanical contact leads to energy transfer in the form of work, denoted ‘W ’; thermal contact leads to energy transfer in the form of heat, denoted ‘Q’. For our purposes, these are the only means of energy transfer between system and
surroundings. This leads to the revised
First Law: Under any thermodynamic change,
ΔU = Q + W . [always] (7.3)
Note that positive Q and W lead to increased U, reflecting a focus on the system. Engineers often focus on the surroundings, leading to the opposite sign convention (at least for W ). Note also that Equations (7.2) and (7.3) mply the following useful relations: