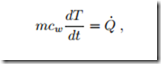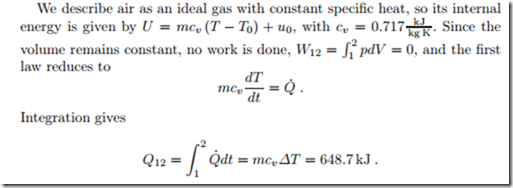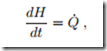Example: Heating Problems
Heating of Water
2 litre of water at T1 = 20 ◦C are heated in a well isolated 2 kW electric kettle. We compute the time required to heat the water to T2 = 90 ◦C.
In this temperature range, liquid water can be well described as an incompressible liquid with mass density ρ = 1000 kg and constant specific heat cw = 4.18 kJ . The mass of water in the heater is m = ρV = 2 kg. Since the volume of the water remains unchanged, there is no work done, and with the internal energy U = mcw (T − T0) + u0, the first law reduces to
with Q˙ = 2 kW as given. Separation of variables and integration over the duration of the process gives mcw (T2 − T1) = Q˙ (t2 − t1), or
For the unit conversion we have used that 1 kW = 1 kJ .
Heating of Water with Heat Loss
We consider the same problem as above, only that now the water in the heater loses heat to the environment at T0 = 20 ◦C at a rate of Q˙ loss = α (T − T0) with a transfer coefficient α = 25 W . The heat loss must be added to the heat supplied by the kettle, so that the first law reads (careful with the sign, the heat loss must be subtracted)
The heat transfer coefficient α depends on the material, and the system configuration. Our sense of cold or hot is not a sense of temperature, but rather a sense of heat transfer. When we touch an object with large heat transfer coefficient, a large amount of heat is exchanged between our hand and the object, which feels hotter or colder as an object with smaller heat transfer coefficient at the same temperature. The amount of energy available plays a role as well. A larger amount of heat can be transferred to our hand from an object with large thermal mass mc. Wood feels not as cold as metal of the same temperature.
Isochoric Heating of an Ideal Gas
We consider the air-filled room from a previous example which contains 180.94 kg of air, initially at 20 ◦C, 1 atm. We now assume the room is perfectly sealed, so that the air volume remains constant, and ask for the total amount of heat that must be supplied to heat the room to 25 ◦C.
A 2 kW heater would need Δt = Q12/Q˙ = 324 s to heat the air in the room by 5 ◦C. The heating of a real room takes longer, since a substantial amount of heat is required to heat the walls, which have a large thermal mass mc, moreover one will expect heat loss through the walls to the colder outside environment.
The pressure after heating is completed, p2, follows from the ideal gas law pV = mRT . Since mass and volume remain constant we have p/T = mR/V = const, so that p2/T2 = p1/T1 or p2 = p1T2/T1 = 1.017 atm = 1.0305 bar (temperatures in Kelvin!).
Isobaric Heating of an Ideal Gas
Next we ask for the amount of heat required to heat the same amount of air under constant pressure.
In this case, the heat is best computed from the alternative form (3.20) which for constant pressure reduces to
where H = mh is the enthalpy of the enclosed air, with h = cp (T − T0)+ h0 and cp = 1.004 kJ . Integration gives
A 2 kW heater would need Δt = Q12/Q˙ = 454 s to heat the air in the room, provided that no heat loss occurs to and through the walls.
The initial volume is V1 = 150 m3 and the volume after heating follows from the ideal gas law pV = mRT . Since pressure and mass remain constant, we have V2/T2 = V1/T1 and find V2 = V1T2/T1 = 152.6 m3. The expansion of the air requires moving boundary work. Since pressure is constant we find
In the isochoric case all heat supplied goes to increase the internal energy. The heat required for isobaric heating is bigger since, while the increase of internal energy is the same, additional energy is required to provide the expansion work.