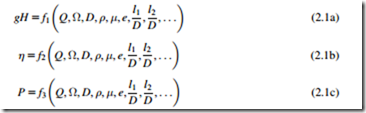Incompressible fluid analysis
The performance of a turbomachine can be expressed in terms of the control variables, geometric variables, and fluid properties. Take as an example a hydraulic pump. It is convenient to regard the
net energy transfer, gH; the efficiency; η; and the power supplied, P, as dependent variables and to write the three functional relationships as
For a family of geometrically similar machines, the shape parameters, l1/D and l2/D are constant and may be omitted. Dimensional analysis1 can then be applied to determine the dimensionless groups that are needed to describe dynamic similarity. The number of dimensionless groups required can be found using Buckingham’s π-theorem (Buckingham, 1914). This theorem states that for M independent variables and N dimensions, there must be at least M 2 N nondimensional groups. In this case, for 6 variables ðQ; Ω; D; ρ; μ; eÞ and 3 dimensions (mass, length, time), there must be 6 2 3 5 3 independent nondimensional groups. However, the form of the nondimensional groups required is not obvious and consideration of the physics is necessary. For a pump, the selection of ρ, Ω, and D as common factors avoids the appearance of special fluid terms (e.g., μ, Q) in more than one group and allows gH, η, and P to be made explicit. Hence, the three relationships in Eqs. (2.1a-c) can be reduced to the following easily verified forms:
Energy transfer coefficient, sometimes called head coefficient:
Both of these nondimensional groups are usually referred to as a flow coefficient, Φ.
The nondimensional group ρΩD2/μ is a form of Reynolds number, denoted Re. Physically, Reynolds number represents the ratio between the inertial forces and the viscous forces within a fluid flow. For low viscosity fluid moving at high velocity, the Reynolds number is high; conversely for slow moving fluid with high viscosity, the Reynolds number is low. It is found experimentally that provided Re . 2 3 105, the effects of Re on the performance of turboma- chines is small. This is true because at high Re, the viscous boundary layers on the blades of a turbomachine are generally turbulent and very thin. They, therefore, have little impact on the global flow field. Efficiency is the variable that can be most affected by Reynolds number and typically η will rise up to a few per cent as Re increases an order of magnitude. Note that for turbomachines handling water, the kinematic viscosity, ν 5 μ/ρ, is very small and, therefore, the corresponding Reynolds number is always high and its effects may be ignored to a first approximation.
The effects of surface finish are captured by the nondimensional group, e=D, called the rough- ness ratio or relative roughness. At high Reynolds numbers, greater surface roughness tends to increase skin friction losses and thus reduce the efficiency. The effects at lower Reynolds numbers are more complex as the boundary layers may be laminar or undergoing transition to turbulence. If it is assumed that both the surface finish effects are small and that the Reynolds numbers are high, the functional relationships for geometrically similar hydraulic turbomachines are:
This is as far as the reasoning with dimensional analysis alone can be taken; the actual form of the functions f4, f5, and f6 must be ascertained by experiment.
One relation between ψ, Φ, η, and P^ may be immediately stated. For a pump, the net hydraulic power, PN, equals ρQgH, which is the minimum shaft power required in the absence of all losses.
As shown in Chapter 1, we define pump efficiency as η 5 PN=P 5 ρQgH=P, where P is the actual power to drive the pump. Therefore,
Thus, f6 may be derived from f4 and f5 since P^ 5 Φψ=η. For a turbine, the net hydraulic power supplied to it, PN, is clearly greater than the actual power output from the machine and the efficiency η 5 P=PN. By reasoning similar to that provided for the pump, we can see that for a turbine P^ 5 Φψη.