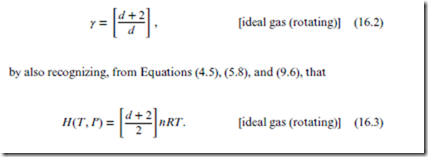Crazy Gay-Lussac’s Gas Expansion Emporium
Sales Pitch
You want gas expansions? Crazy Gay-Lussac’s got ’em—in all models, shapes, and sizes, and so cheap he’s practically giving them away. So come on down to Crazy Gay-Lussac’s Gas Expansion Emporium today! Even if the above hype does not exactly get you excited about them, gas expansions are indeed the oldest and most universal application of thermodynamics. Moreover, they are still very relevant today: still used routinely in engineering practice; still taught in virtually every thermodynamics course regardless of discipline; still embodying core thermodynamics principles. Accordingly, gas expansions are the one from a myriad of applications that appears in this book (but see Chapter 17…).
As alluded to above and in Section 8.5, gas expansions do indeed come in a great many flavors—so many that when solving problems, it can be difficult to know where to begin. Part of our job in this chapter is thus to sort through all of this variety for you, thereby serving as a (hopefully) useful reference. In particular, Section 16.3 provides a “comprehensive compendium” of increasingly specific results, presented in outline form.
On the other hand, our larger mission (as always) is to convey a sense of how to approach problems systematically. Section 16.2 thus provides the tools needed to tackle any gas expansion, without resorting to memorization of all the special cases.
⊳⊳⊳ Helpful Hint: While reading this chapter, you may find it helpful to refer to certain previous material, such as: Fig. 7.1 (p. 50); Sec. 7.2 (especially Helpful Hints); Fig. 8.1 (p. 58); Don’t Try Its on p. 59; box on p. 60; Fig. 8.2 (p. 61); Sec. 8.5; Sec. 9.2; Log Blog posts on p. 63 and p. 83; Fig.13.1 and surrounding discussion (p. 108).
How to Solve Gas Expansion Problems
The “zeroth” step in solving a gas expansion problem is to identify the type of gas expansion that it is—with respect to the following four attributes:
All of these attributes or conditions have been defined previously—e.g., in Section 8.5.
With one choice for each of the four attributes in the box above, 24 distinct gas expansion types emerge in all—though in practice, not all of these are realized. Also, certain types (e.g., reversible, non-free, isothermal, ideal) are seen much more frequently—the everyday specials! The remaining steps are outlined below; these need not be followed exactly, but serve as a guideline:
In Step 1, the second variable should obviously be T for an isothermal expansion, or P or Psur for an isobaric expansion; in both cases, the constant nature of the variable should be exploited to make the problem easier to solve. Steps 2 and 3 above use the fact that for both the initial and final states, the system is in equilibrium (Section 8.4). This also implies that Psur(Vi) = Pi and Psur(Vf ) = Pf . This is true for all gas expansions (including irreversible ones). Step 4 is the only integration that is usually required; from W , the quantities Q and ΔSsur can be obtained, in Steps 5 and 6, respectively.
Adiabatic expansion: This case is tricky, because all three variables can change. The strategy is thus to exploit Q = 0—leading, e.g., to ΔSsur = 0, and to a simple expression for work that does not require integration (W = ΔU).
These steps are easier than for the isothermal and isobaric cases, but Step 2 is harder.
Reversible adiabatic expansion of ideal gas: Here, Step 2 can be achieved by following an adiabat, P(V ) ∝ V −(Section 13.1, Figure 13.1, and Figure 13.2), where the adiabat coefficient is the heat capacity ratio (p. 70). The proof requires Equation (11.9), whose generalization for rotating ideal gases is as follows:
Note that d is the total number of coordinates per molecule, including the rotational coordinates (see discussion and box on p. 40). Since S is constant (Section 11.5), so must be V (PV )d∕2, and also PV (d+2)∕d . Finally, from the box on p. 69 we can identify
Isobaric expansion: Generally, this condition can be regarded as Psur = const = Pf —the gas is expanded against a constant surroundings pressure equal to the final system pressure, resulting in W = −Pf ΔV . For reversible isobaric expansion, Pi = P = Psur, and T changes in accord with the equation of state. More interesting is irreversible isobaric expansion—arising (for true expansion) when Pi > Psur, after the system and surroundings are brought into mechanical contact. The irreversible case can be—and often is—also isothermal. If so, then all system state function ΔX values are identical to those of the corresponding reversible isothermal expansion, since the initial and final states for the two paths are identical. This can save time on Free expansion: This occurs when the partition between two chambers— one containing gas and the other empty—is suddenly ruptured or removed.
Since Psur = W = 0 (p. 58), the expansion ends not when Pf = Psur, but rather, when the gas reaches the expanded limits of the container. All free expansions are true expansions (ΔV > 0), and also irreversible. They can be isothermal or adiabatic—with these two special cases being identical to each other for the ideal gas (ΔT = 0 = ΔU = Q + W ).
Ideal gas: There are many important results that can be derived explicitly for the ideal gas. Many of these have already been provided in this book, for the ideal gas of point particles. As this chapter deals with rotating ideal gases however, we need more general expressions. In addition to those presented above, the following equations—derived from Equations (5.8) and (16.3), respectively—will also prove useful, particularly for the com- pendium (Section 16.3):
Comprehensive Compendium
The following comprehensive compendium of gas expansions is presented in outline form, with more specific conditions corresponding to greater indentation. To use the compendium, first identify the particular type of gas expansion, as per the box on p. 132. Then scan downward until you reach an attribute (e.g., “Reversible”): if it applies, keep scanning down; otherwise, jump to the next attribute that appears at the same indentation level. All entries encountered in this fashion will apply to your particular gas expansion.
⊳⊳⊳Try It !! Try to derive the compendium results on your own! Each entry includes a brief description: in some cases, this is all you need to derive the result; in other cases, you may need to do a bit more work…