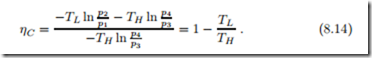Thermodynamic Cycles
In previous chapters we discussed thermal efficiency of heat engines and co- efficient of performance of refrigerators and heat pumps from a general view- point, without asking for the processes occurring within the engines. Now we will discuss the working principles of several closed system cycles.
All engines considered are steady state devices that do not accumulate energy or mass over time. To realize a steady state thermodynamic engine, a working fluid is subjected to a series of processes such that the process curve in a property diagram forms a closed loop. As the engine operates, the working fluid runs through the same cycle of processes again and again.
The closed loop integral of the energy vanishes, cf dE = 0, since energy is a state property;1 the engine does not accumulate energy. Thus, integration of the differential energy balance dE = δQ − δW over the full cycle yields
where W8 and Q8 are the total net work and net heat exchanged for the cycle. Moreover, Qin > 0 is the total heat transferred into the cycle, and Qout < 0 is the total heat transferred out.
Net work and net heat are positive for a clockwise process—a heat engine— and are negative for a counter-clockwise process—a refrigerator or a heat pump.
For a closed system, the engine contains the constant mass m of the working substance, and the net work and heat per unit mass are
For an engine that runs through the cycle with the frequency n˙ (measured
for instance in rounds per minute, rpm) the net power and the heat transfer rates are
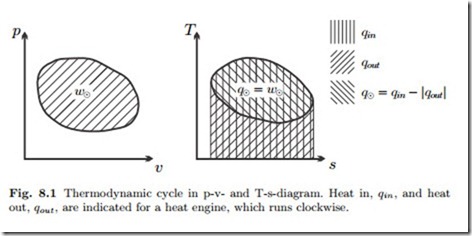
Figure 8.1 shows a reversible thermodynamic cycle in the p-v- and T-s- diagrams. For a reversible process in a closed system, the net work of the cycle per unit mass of working fluid is
In the p-v-diagram, the net work is just the area enclosed by the process curve as indicated in the figure. Note that the integral is positive for a clockwise cycle, and negative for a counter-clockwise cycle.
Similarly, the net heat exchanged for a reversible cycle is the area enclosed by the cycle in the T-s-diagram,
can be read from the T-s-diagram as the areas below the respective process curves. This is indicated in the figure for a heat engine (clockwise cycle). With this, the net work (w8 = q8), the heat in, and the heat out can all be read from the T-s-diagram. This implies that the thermal efficiency or the coefficient of performance for a reversible cycle can be completely determined from the T-s-diagram, by means of the relations
While in this chapter we discuss only reversible cycles, we note that the processes in real engines always suffer from irreversibilities, so that their thermal efficiencies or COP’s will be smaller than those that will be computed below.
Carnot Cycle
As a first example for the evaluation of a thermodynamic cycle we consider the Carnot cycle. We introduced the Carnot engine as a fully reversible engine— no internal or external irreversibilities—operating between two reservoirs of temperatures TH , TL. The Carnot cycle is one possible realization of such an engine. For a heat engine, it consists of the following four processes
1-2 rev. isothermal compression at TL
2-3 rev. adiabatic (isentropic) compression from TL to TH
3-4 rev. isothermal expansion at TH
4-1 rev. adiabatic (isentropic) expansion from TH to TL
Heat is only exchanged with the reservoirs during the isothermal processes, at which the working substance is at the temperature of the reservoirs, and therefore there are no external irreversibilities associated with the cycle. Since there are no internal or external irreversibilities, the above cycle is a fully reversible cycle that exchanges heat only with the two reservoirs.
The T-s-diagram allows us to compute the thermal efficiency of the cycle: The area enclosed by the cycle is the net work,
Accordingly, the thermal efficiency is, as expected, the Carnot efficiency
With the above results for work and heat, and the relation between the pressures, we find, once more, the Carnot efficiency,
That we found the well-known result again from detailed calculations for an ideal gas proves that the ideal gas temperature scale (Sec. 2.13) is identical to the thermodynamic temperature scale (Sec. 5.6).
The net work of the ideal gas Carnot cycle,
grows with the temperature difference (TH − TL) and the pressure ratio p2 . Thus, for large efficiency and large work output the Carnot cycle should operate at large temperature difference TH − TL and at large pressure ratios p2 . Then, the volume ratio between smallest and largest volume,2 v1 = p2 ( TH k−1 , becomes large, which is quite unpractical for designing a compact engine. Moreover, the overall pressure ratio p3 = v1 TH becomes large, which makes effective sealing difficult. For example, an engine with air as working gas operating at TL = 300 K, TH = 750 K, and a pressure volume ratio v1 = 49.5, and the overall pressure ratio p3 = 124; it produces the net work w8 = 208 kg . Internal combustion engines with comparable net work operate with significantly smaller volume and pressure ratios, and thus are more compact and lighter, and suffer less from sealing problems.
Another problem for the Carnot cycle is that the isothermal heat exchange processes (1-2, 3-4) require slow processes, so that the cycle frequency n˙ must be low. To produce significant amounts of power W˙ = n˙ mw8 the engine would have to contain a large mass m, that is it must be large. Engines that operate on higher frequencies n˙ can be more compact.
The Carnot engine operates between two reservoirs of constant temperature. If the engine is to be heated by burning of a fuel, one does not have a constant high temperature reservoir, but a flow of hot combustion product at flame temperature TF which is gradually cooled to TH in the heat exchange.
This implies that there will be a temperature difference between engine and combustion gas, and thus an external irreversibility. If one uses such a hot flow to heat the engine, one will have warm exhaust which has still work potential. If the exhaust is expelled into the environment, the equilibration of temperature between the warm exhaust (at TH or higher) and the environment (at TL or lower) is an external irreversibility. To eliminate, or at least reduce this loss, the exhaust must be used for preheating of the combustion air. We shall come back to this point in Secs. 11.7 and 12.1.
In principle, one could make an effort to design an engine that follows the Carnot cycle. Obviously, due to irreversibilities, the real engine would have an efficiency below the Carnot efficiency. Moreover, for the reasons listed above, such an engine would be relatively large and heavy in relation to the amount of power it could deliver. Thus, in fact, one does not try to build engines that follow the Carnot cycle for practical applications.
The Stirling cycle with an ideal gas, which will be discussed in Sec. 13.1, is an alternative realization of a Carnot engine, but compared to the Carnot cycle it has a significantly smaller volume ratio. Stirling engines, i.e., engines designed to follow the Stirling cycle, are commercially available. Naturally, these have efficiencies below the Carnot efficiency due to unavoidable internal and external irreversibilities.