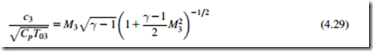Preliminary axial turbine design
The process of choosing the best turbine design for a given application involves juggling several parameters that may be of equal importance, for instance, rotor stress, weight, outside diameter, efficiency, noise, durability, and cost, so that the final design lies within acceptable limits for each parameter. In consequence, a simple presentation can hardly do justice to the real problem of an integrated turbine design. However, a consideration of how the preliminary design choices affect the turbine basic layout and the efficiency can provide useful guidance to the designer.
As demonstrated earlier in the chapter, the main goal in the preliminary stage design of a turbine is to fix the shapes of the velocity triangles, either by setting the flow angles or by choosing values for the three dimensionless design parameters, φ, ψ, and R. If we now consider matching the overall (dimensioned) requirements of the turbine to the velocity triangle parameters, the general layout of the turbomachine can also be determined.
Number of stages
First, from the specification of the turbine, the design will usually have a known mass flow rate of the working fluid and a required power output. This enables the specific work output of the turbine to be calculated according to ΔW 5 W_ =m_ . The specific work per stage can be determined from the stage loading and the blade speed and, thus, the required number of stages can be found as
An inequality is used in Eq. (4.22) since the number of stages must be an integer value. The result shows how a large stage loading can reduce the number of stages required in a multistage turbine. It also shows that a high blade speed, U, is desirable. However, this is usually constrained by a stress limit, because centripetal loadings and vibration rise rapidly with rotor speed, see later in this chapter. In some cases, aerodynamic or acoustic considerations may limit the maximum blade speed. For example, if a turbine is required to operate with transonic flow, the blade speed may be constrained by the need to limit the maximum flow Mach number.
Blade height and mean radius
Given that the axial velocity remains constant throughout each stage, i.e., cx1 5 cx2 5 cx3 5 cx, then the continuity equation for the turbine, Eq. (4.1), reduces to
This equation is only approximate since it assumes the mean radius is exactly midway between the hub and tip, i.e., rm 5 (rt 1 rh)/2. To be precise, the mean radius should be the radius that divides the annulus into two equal areas, i.e., r2 5 ðr2 1 r2Þ=2. However, for high hub-to-tip radius ratios these definitions of mean radius are equivalent. In all cases, an accurate expression for the annulus area is given by
This equation is useful for determining the annulus area if the hub-to-tip radius ratio required for the turbine is known or if the casing diameter is set by the need to fit the machine in with other components.
Often, the mean radius will be fixed by the need to rotate at a particular rotational speed (e.g., for mains electricity, Ω 5 50 Hz 5 3000 rpm) and using a known blade speed, rm 5 U/Ω. The span- wise height required for the blades can then be determined from
In compressible gas turbines, the inlet stagnation conditions and the inlet Mach number may be known. This then fixes the inlet annulus area via the mass flow function:
The area found from this can then be used with Eq. (4.24) or (4.25) to find the blade span. For the subsequent, downstream stage, the stagnation temperature and pressure can be found from the following relationship for the stage loading and pressure ratio:
Note that the polytropic efficiency is used here since this is more appropriate for calculating changes in properties across a single stage. The Mach number at inlet to the downstream stage can then be found from the velocity using the following compressible flow relationship (included in the compressible flow tables):
The new annulus area is then determined from Eq. (4.27) and, given the fact that the mean radius is constant, the blade span can be found. This process can be repeated for subsequent stages, enabling the general arrangement of the entire turbine to be determined in terms of the size and number of stages.
Number of aerofoils and axial chord
The number of aerofoils in each turbine row and the chord lengths of the vanes and blades can also be estimated during the preliminary design. The aspect ratio of a blade row is the height, or blade span, divided by the axial chord, H/b. A suitable value of this is set by mechanical and manufacturing considerations and will vary between applications. For jet engine, core turbines aspect ratios between 1 and 2 are usual, but low-pressure turbines and steam turbines can have much higher values, as demonstrated in Figures 4.1 and 4.2. To find the ratio of blade pitch to axial chord, s/b, the Zweifel criterion for blade loading can be applied, as detailed in Chapter 3. Equations (3.51) and (3.52) show how, given the turbine velocity triangles, the pitch to axial chord ratio can be found from an optimum value of Zweifel coefficient. For a known axial chord, knowing s/b fixes the number of aerofoils.