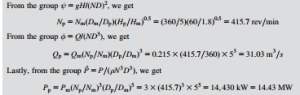Effect of size on turbomachine efficiency
Despite careful attention to detail at the design stage and during manufacture, it is a fact that small turbomachines always have lower efficiencies than larger geometrically similar machines. The pri- mary reason for this is that it is not possible to establish perfect dynamical similarity between turbomachines of different size. To obtain this condition, each of the dimensionless terms in Eq. (2.2) would need to be the same for all sizes of a machine.
To illustrate this, consider a family of turbomachines where the loading term, ψ 5 gH/Ω2D2, is the same and the Reynolds number, Re 5 ΩD2/ν, is the same for every size of machine, then
must be the same for the whole family. Thus, for a given fluid (v is a constant), a reduction in size D must be followed by an increase in the head H. A turbine model of one-eighth the size of a prototype would need to be tested with a head 64 times that required by the prototype! Fortunately, the effect on the model efficiency caused by changing the Reynolds number is not large. In practice, models are normally tested at conveniently low heads and an empirical correction is applied to the efficiency.
With model testing, other factors affect the results. Exact geometric similarity cannot be achieved for the following reasons:
a. The blades in the model will probably be thicker than in the prototype.
b. The relative surface roughness for the model blades will be greater.
c. Leakage losses around the blade tips of the model will be relatively greater as a result of increased relative tip clearances.
Various simple corrections have been devised (see Addison, 1964) to allow for the effects of size (or scale) on the efficiency. One of the simplest and best known is that due to Moody and Zowski (1969), also reported by Addison (1964) and Massey (1979), which as applied to the efficiency of reaction turbines is
where the subscripts p and m refer to prototype and model, respectively, and the index n is in the range 0.2-0.25. From comparison of field tests of large units with model tests, Moody and Zowski
concluded that the best value for n was approximately 0.2 rather than 0.25 and for general application this is the value used. However, Addison (1964) reported tests done on a full-scale Francis turbine and a model made to a scale of 1-4.54 that gave measured values of the maximum efficiencies of 0.85 and 0.90 for the model and full-scale turbines, respectively, which agreed very well with the ratio computed with n 5 0.25 in the Moody formula!
EXAMPLE 9.6
A model of a Francis turbine is built to a scale of one-fifth of full size and when tested it developed a power output of 3 kW under a head of 1.8 m of water, at a rotational speed of 360 rpm and a flow rate of 0.215 m3/s. Estimate the speed, flow rate, and power of the full-scale turbine when working under dynamically similar conditions with a head of 60 m of water.
By making a suitable correction for scale effects, determine the efficiency and the power of the full-size turbine. Use Moody’s formula and assume n 5 0.25.
Solution
This result has still to be corrected to allow for scale effects. First we must calculate the efficiency of the model turbine. The efficiency is found from