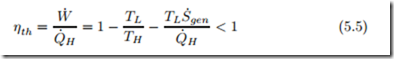Heat Engines
First we consider power generation, that is the conversion of heat into work in a heat engine, so that W˙ = W˙ > 0. Elimination of Q˙ L between the first and second law (5.1) gives the work
Since we require W˙ > 0, the right hand side of this equation must be positive as well. The last term, −TLS˙gen, is zero or negative, since thermodynamic temperature and entropy generation rate are both non-negative; therefore, the first term, /1 − TL Q˙ H , must be positive. Since the bracket is always positive, this implies positive heat input from the hot reservoir, 
0. The heat rejected to the colder reservoir is 
Figure 5.2 shows the direction of heat and work flow for a heat engine between the reservoirs.
According to (5.2), for given TH , TL, the work output is larger for smaller entropy generation rate S˙gen ≥ 0. Entropy generation is due to heat transfer and friction processes within the engine, and between engine and reservoirs, and cannot be totally avoided in real engines. Instead, the engineering task is to minimize entropy generation within the system as much as possible, in order to achieve the best possible performance of the engine. The work loss to irreversibilities is proportional to the entropy generation,
The theoretical limit for the power generated from two reservoirs with constant temperatures is obtained for S˙gen = 0, that is for a fully reversible engine, as
This is the work output of a Carnot engine, named after Sadi Carnot (1796- 1832), who established this theoretical limit. Any entropy generation S˙gen in the engine reduces the work output by TLS˙gen.
To quantify the performance of engines, it is useful to define dimensionless efficiency measures that compare the output (“what you get”) to the input (“what you pay for”). For heat engines, accordingly, one defines the thermal efficiency ηth as the ratio between work output and heat input. For heat engines operating between two reservoirs, we obtain
for the Carnot engine.
The Carnot efficiency ηC is the efficiency of a fully reversible engine operating between two reservoirs at constant temperatures. Since it was computed from general considerations, its value is completely independent of the details of the engine, i.e., it does not depend on the working fluid used, nor on the realization of the engine. The Carnot efficiency is a universal limit for the thermal efficiency any engine operating between two reservoirs at TH , TL can have. We summarize the above in two statements:
(a) The thermal efficiency of a fully reversible engine operating between two reservoirs is independent of the realization of the engine; it is given by the Carnot efficiency ηC .
(b) Any engine operating between two reservoirs in which irreversible processes occur has a thermal efficiency below that of a fully reversible engine.
The amount of work produced grows with the temperature ratio TH /TL between the reservoirs. In technical energy conversion processes one will aim for high upper temperature TH to ensure high energy conversion efficiency. At high temperatures material strength is limited, so that the upper temperatures are limited through the materials used for building the engines. Typically, the lower temperature TL is the temperature of the environment, T0.
For temperature ratios TH /TL close to unity, i.e., small temperature differences, the thermal efficiency is small, and only little power can be produced. Hence, low temperature waste heat (low TH ) is relatively useless for power production, and, if possible, should rather be used for space heating. High temperature waste heat (high TH ), however, has considerable work potential that should be used. In other words:
Energy at high temperature is more valuable than energy at low temperature, since more work can be extracted from it.