Examples
Isochoric Process for Ideal Gas
Carbon dioxide is confined in a 10 litre tank at a pressure of p1 = 10 bar. In an isochoric heat transfer process the temperature drops from T1 = 670 K to T2 = 25 ◦C. We compute the heat transferred from the system and the entropy change.
Isochoric Heating of Water
Saturated liquid-vapor mix at 100 ◦C with quality x = 0.1 is isochorically heated until the pressure is 2.5 MPa. We compute the final state, and the heat supplied per unit mass.
From a steam table we find initial volume, specific energy and specific entropy as
Isobaric Heating of Ideal Gas
200 kg of air are isobarically heated from the initial state p1 = 15 bar, T1 = 440 K until the volume has doubled. We compute the final state, the heat supplied, and the work done by the gas.
The initial volume is
Isobaric Cooling of R134a
Superheated cooling fluid R134a at initial state p1 = 0.18 MPa and T1 = 40 ◦C is isobarically cooled until the temperature is T2 = −24 ◦C. We determine initial and end state properties, the heat transfer per unit mass, and the work per unit mass.
From a vapor table we find the initial data as
The saturation temperature for 0.18 MPa is Tsat = −12.7 ◦C and since the final temperature lies below this value, the final state is compressed liquid. We use the approximations for compressed liquid to determine1
Isentropic Compression of Ideal Gas
We consider the isentropic (adiabatic reversible) compression of air with a compression ratio V1/V2 = 8. The initial state of the air is T1 = 290 K and p1 = 95 kPa, so that s0 = s0 (T1) = 7.103 kJ (from the Table in Fig. 6.17). The final temperature must be obtained from (7.19), which reads
To find the proper temperature value when vr is not provided in a table, one has to use trial and error. A first guess can be obtained from assuming
Reversible and Irreversible Adiabatic Expansion
Reversible processes require control over the process at all times. The slow expansion of a gas in a piston-cylinder system is the prototypical example for reversible processes.
To further our understanding, we consider the adiabatic expansion— reversible and irreversible—of air as ideal gas at initial state p1 = 10 bar, T1 = 500 K to an end state of half the pressure, so that p2 = 1 p1.
For the adiabatic reversible case we can refer to the above table which tells us that
The table in Fig. 6.17 gives pr (T1 = 500 K) = 6.202, hence pr (T2) = 3.101, and interpolation in the table yields T2 = 412 K.
The tabulated relative pressure simplifies the determination of the final state. We now show how one has to proceed when pr is not in the table: The
We compare the reversible adiabatic process to the fully irreversible process, which was discussed in Secs. 3.13, 4.13. There we saw that the temperature of the ideal gas remained constant. If the initial and final pressures are the same as for the reversible process, we compute the change of entropy as
In the irreversible process no useful work is produced and entropy is generated.
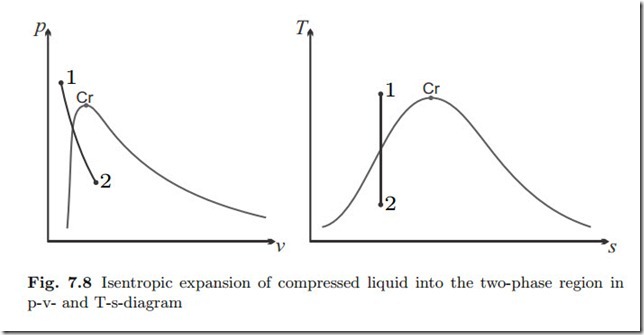
Isentropic Expansion of Compressed Water
Water at T1 = 300 ◦C, p1 = 20 MPa expands in an isentropic (adiabatic and reversible) process to p2 = 1 atm. We determine the final temperature, the volume change, and the work.
The saturation temperature for the initial pressure is Tsat (p1) = 365.8 ◦C > T1. Accordingly the initial state is compressed liquid. As will be seen, the process ends in the two phase region. Figure 7.8 shows the p-v- and T-s-diagrams.
From the property table in Fig. 6.16 we find the initial properties
while the approximations of Sec. 6.9 give
Isothermal Expansion of Steam
Water vapor at p1 = 200 bar and T = 400 ◦C is isothermally expanded to p2 = 1 bar. To determine work and heat we require internal energy and entropy at the two states. From a steam table we find
We see clear differences, in particular for the heat q12, which are due to real gas effects. Clearly, the assumption of ideal gas behavior of steam at these conditions is not justified.
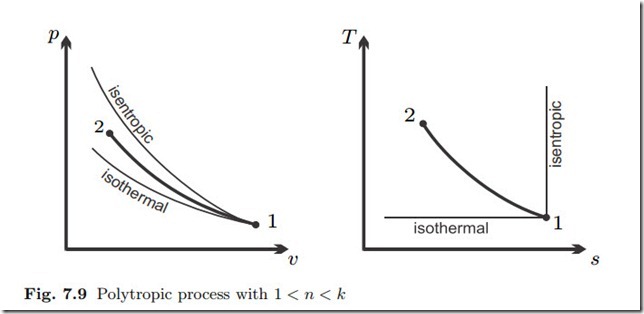
Polytropic Process
The heat removed from the system follows, with U = mcv (T − T0), as
Thus, in this compression process, entropy decreases, and temperature grows, as indicated in the diagram.