Problems
A Heat Engine
A heat engine that operates between two reservoirs at TH = 500 ◦C and TL = 25 ◦C produces 1.25 MW of power from a heat intake of 2.5 MW.
Compute the heat rejected, the thermal efficiency, the entropy generation rate, the work loss to irreversibilities, and the 2nd law efficiency of the engine.
A Heat Pump
An off-the-shelf heat pump system has a COP of 3.4 for operation between 25 ◦C and −5 ◦C. Determine the entropy generation per kW of heating, the percentage of power consumed required to overcome irreversibilities, and the 2nd law efficiency of the system.
A Refrigerator
A refrigeration system has a COP of 2 for operation between 20 ◦C and −10 ◦C and consumes 1.5 kW of electrical power. Determine the second law efficiency of the system, the entropy generation rate, and the amount of power required to overcome irreversibilities.
Heating of House
A small house is exposed to an environment of T0 = −5 ◦C, the temperature inside is to be maintained at Th = 22 ◦C. The heat loss is given by Newton laws of cooling as Q˙ loss = αA(Th − T0), where A = 260 m2 is the outside surface of the house and α = 1 W is an overall heat transfer coefficient. Determine the amount of electrical work for heating the house for the following cases:
1. With a resistance heater.
2. With an internally and externally reversible Carnot heat pump.
3. With an externally irreversible Carnot heat pump with 15 K temperature difference for heat transfer.
Space Heating
A friend who is going to build a house asks you for advice on heating systems. His contractor has offered the following choices: (a) baseboard resistance heaters, (b) heat pump with hot water radiators (circulating water heated to 60 ◦C), (c) heat pump with warm water floor heating (circulating water heated to 35 ◦C).
Based on your knowledge of thermodynamics, which option should your friend chose? Present your arguments. Assume outside temperature −10 ◦C and inside temperature 20 ◦C.
A Cycle
A closed piston-cylinder engine with helium as working medium operates on the following reversible cycle
1-2: Isentropic compression from p1 = 10 bar, T1 = 300 K 2-3: Isobaric heat addition until T3 = 1200 K
3-1: Isochoric cooling to the initial state
1. Draw p-V-diagram and T-s-diagram for the cycle.
2. Determine the thermal efficiency of the cycle and the net work output per unit mass.
3. How much work per unit mass could be obtained from the heat rejected into the environment in the best case? Assume the environment is at T0 = 300 K, p0 = 1 bar.
Exhaust of a Car Engine
The engine of a car delivers a net work of 848.4 kJ from an heat intake of 1520.4 kJ (reversible operation). The state at the end of the expansion stroke of the engine is 1146.6K and 3.822 bar. In the engine, air in this state is exhausted into the environment which is at 300 K, 1 bar.
The exhaust process is modelled as isochoric cooling to the environment. Use the combined first and second law to compute the amount of work that could be obtained from the exhaust in a fully reversible process and compare to the work delivered by the engine.
What would be the thermal efficiencies for the engine alone, and for a system that also provides the work obtainable from the exhaust?
Exhaust of a Car Engine (Continuous)
The state at the end of the expansion stroke of a car engine is 1140 K and 3.8 bar. In the actual engine, air in this state is exhausted into the environment which is at 300 K, 1 bar.
Assume that the exhaust is leaving the engine as a continuous steady flow, and determine the work that could be obtained from the exhaust in a fully reversible process. Compare to the work delivered by the engine.
Use of Waste Heat
A chemical plant rejects 2 MW of waste heat at 350 ◦C and 4 MW at 200 ◦C.
Moreover the plant consumes 5 MW of electrical energy. In the past, the waste heat was just dumped into the environment (20 ◦C), but now there is a plan to use it for power production to reduce the electricity bill. Estimate what percentage of the electric power consumed in the plant could be produced by a suitable system, when 20% of the maximum possible is lost to irreversibilities.
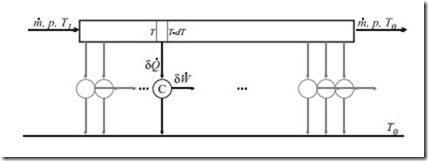
Reversible Heat Transfer
Consider a steady state isobaric flow (pressure p, mass flow m˙ ) of a fluid that enters the system at a temperature T1 and leaves at the environmental temperature T0. The heat withdrawn is used to drive a series of infinitely many infinitesimal Carnot engines. All processes are fully reversible. Compute the total power output of the system.
Entropy Generation in Mixing
In an adiabatic mixing chamber, a mass flow of 200 kg compressed liquid water at 10 bar, 40 ◦C is mixed isobarically with saturated steam so that the exiting flow is in the saturated liquid state. Determine the mass flow of saturated steam that must be added, the entropy generation rate, and the work loss for the process (with respect to standard environment).
Entropy Generation in Steam Generator
The temperature in the boiler of a big steam power plant is constant at 700 ◦C. The pipes of the steam generator run trough the boiler, with the inlet state being compressed liquid at 200 bar, 50 ◦C, and the exit state being at 200 bar, 550 ◦C. For a mass flow of 1150 t , determine the heating rate, the entropy generation rate and the associated work loss (with respect to standard environment).
Entropy Generation in Steam Generator
Consider a 250 MW nuclear power plant with thermal efficiency of 0.32. The steam generator is kept at a pressure of 17.5 MPa. The incoming feedwater is in the compressed liquid state at 40 ◦C, and the exiting steam is superheated vapor at 400 ◦C. The heat is provided by a counter-flow of molten sodium (ideal incompressible liquid, mass density 0.927 g , specific heat 1.26 kJ )
which enters at 500 ◦C and leaves at 350 ◦C.
1. Determine the mass flows of steam and sodium.
2. Determine the total entropy generation rate in steam generator, and the corresponding work loss.
Entropy Generation in Condenser
The condenser of a small steam power plant is kept at a temperature of 45 ◦C.
The inlet state is at a quality of 90%, and the exit state is saturated liquid. The condenser rejects heat to the environment which is at 5 ◦C. For a mass flow of 75 t , determine the cooling rate, the entropy generation rate and the associated work loss.
Entropy Generation in Throttling
Cooling fluid R134a in compressed liquid state at 1 MPa, 26 ◦C is throttled adiabatically to a pressure of 0.14 MPa. For a mass flow of 1 kg , determine the entropy generation rate, and the associated work loss.