Measure of Independence-Closeness Centrality
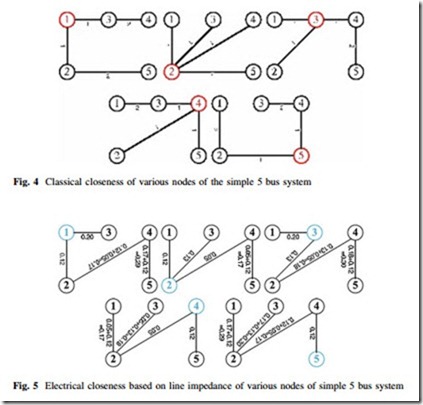
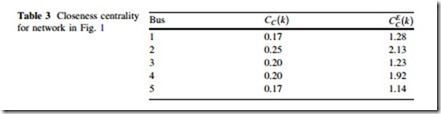
This approach of centrality measure is based upon the degree to which a node is close to all other nodes in the network [3]. Figure 4 shows closeness in a classical sense and to illustrate the idea of electrical closeness centrality, Fig. 5 is drawn to show the closeness of various nodes of the simple 5 bus system in Fig. 1 in terms of electrical distance found in Table 1. It is clear from Fig. 5 that node 2 is adjacent to three other nodes (nodes 1, 3 and 4) in terms of electrical distance, while nodes 1, 3, and 4 being adjacent to two nodes. Node 5 is adjacent to one node only. So node 2 is the closest to other nodes than the rest of the nodes in the network.
In the social network theory, closeness is a sophisticated measure of centrality. It is defined as the mean geodesic distance (i.e., the shortest path) between a vertex k and all other vertices reachable from it [21]. In mathematical form, the closeness centrality of a vertex k, CC ðkÞ in a network of n vertices is given by:
where, dðk; tÞ being the shortest path length between vertices k and t. This definition of closeness centrality gives a measure of distance of particular vertex from other vertices. So, some researchers have used the reciprocal of the shortest path to quantify closeness centrality as follows:
where, dzðk; tÞ is taken as the shortest electrical distance between nodes k and t. Resistance was neglected since they considered only transmission systems; but in order to generalize the concept in both transmission and distribution system we cannot neglect resistance of the network lines, which is a significant portion of the line impedance in case of distribution lines. The numerator was taken as n-1.
This was adopted in (9) to average the distance, but when it comes in the numerator it just scales the parameter. So, in this chapter, we propose our electrical closeness centrality as:
where, dðk; tÞ is the weight of the shortest electrical path from node k to all other nodes t reachable from k.
Table 3 shows the closeness centrality of simple 5 bus system in Fig. 1 in classical as in (10) and proposed approach.
The independence of a node is determined by the closeness centrality of the node [3]. In Fig. 1, node 2 is in direct contact with nodes 1, 3 and 4. It must depend upon node 4 to communicate with node 5. So, node 5 needs only one relayer to communicate with all other nodes of the network. On the other hand, node 1 needs node 2 to communicate with node 4 and both need 2 and 4 to communicate with
node 5. So we can say that node 2 is more independent than node 1. So closeness centrality can be used to quantify independence of various nodes within an electrical power grid.