Flow
Differential pressure flowmeters
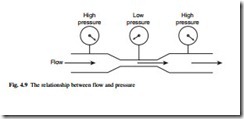
If a constriction is placed in a pipe (Fig. 4.9) the speed must be higher through the restriction to maintain equal mass flow at all points. The energy in a unit mass of fluid has three components which are kinetic energy, potential energy from the height of the fluid and flow energy caused by the fluid pressure. Flow energy is given by P/ρ where P is the pressure and ρ is the density.
In Fig. 4.9 the pipe is horizontal, so the potential energy is the same at all points. As the flow velocity increases through the restriction, the kinetic energy will increase and, for conservation of energy, the flow energy (i.e. the pressure) must fall. Hence eqn 4.5, which is the basis of all differential flowmeters.
Calculation of the actual pressure drop is complex, especially for compressible gases, but is generally of the form:
where K is a constant for the restriction and ∆P is the differential pressure.
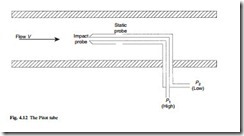
The most common differential pressure flowmeter is the orifice plate shown in Fig. 4.10. This is inserted into the pipe with upstream tapping point at D and down- stream tapping point at D/2 where D is the pipe diameter. The plate should be drilled with a small hole to release bubbles (for liquid flow) or drain condensate (for gas flow). Orifice plates suffer from a loss of pressure on the downstream side; this head loss can be as high as 50 per cent. The Dall tube, shown in Fig. 4.11 has a lower loss of around 5 per cent but is bulky and more expensive. Another low-loss device is the pitot tube (Fig. 4.12).
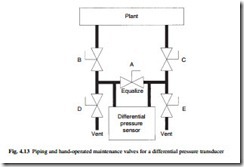
The transmitter should be mounted with a manifold block as shown in Fig. 4.13. Valves B and C are isolation valves. Valve A is an equalizing valve. In normal operation, A is closed and B and C are open. Valves D and E are vent valves used to relieve locked-in pressure prior to the removal of the transmitter.
Conversion of the pressure to an electrical signal requires a differential pressure transmitter and a linearizing square root unit. This square root extraction imposes a
limit on the turndown as zeroing errors are magnified. Although the accuracy and turndown of differential flowmeters is poor (typically 4 per cent and 4:1) they remain the most common type because of their robustness, low cost and ease of installation.
Turbine flowmeters
The arrangement of a turbine flowmeter is shown in Fig. 4.14. Within a specified flow range, (usually with about a 10:1 turndown for liquids, 20:1 for gases,) the rotational speed is directly proportional to the flow velocity. The blades are of ferromagnetic material and pass below a variable reluctance transducer producing an output approximating to a sine wave of the form shown in eqn 4.7.
where A is a constant, ω is the angular velocity and N is the number of blades. Both the output amplitude and the frequency are proportional to the flow, although the frequency is normally used.
Turbine flowmeters are relatively expensive. They are less robust than other flowmeters and are particularly vulnerable to damage from suspended solids. Their main advantages are a linear output and a good turndown ratio, and the pulse output can also be used directly for flow totalization.
Vortex shedding flowmeters
If a bluff body is placed in a flow, vortices detach themselves at regular intervals from the alternate downstream edges as shown in Fig. 4.15. At Reynolds numbers in excess of 1000, the volumetric flow rate is directly proportional to the observed frequency of vortex shedding.
The vortices manifest themselves as sinusoidal pressure changes which can be detected by a sensitive diaphragm on the bluff body or by a downstream modulated ultrasonic beam. The vortex shedding flowmeter can work at low Reynolds numbers, has an excellent turndown (typically 15:1), no moving parts and minimal head loss.
Electromagnetic flowmeters
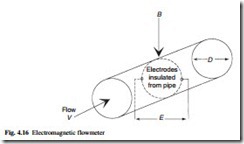
In section 2.2.4 (eqn 2.20) it is seen that when a conductor of length l moves with velocity v perpendicular to a magnetic field of flux density B, the induced voltage is given by Bvl. This principle is used in the electromagnetic flowmeter. In Fig. 4.16 a conductive fluid passes down a pipe with mean velocity v through an insulated pipe section. A magnetic field B is applied perpendicular to the flow. Two electrodes are placed into the pipe sides to form, via the fluid, a moving conductor of length D relative to the field where D is the pipe diameter. A voltage is generated across the electrodes which is proportional to the mean flow velocity across the pipe.
In practice an AC field is used to minimize electrolysis and to reduce errors from DC thermoelectric and electrochemical voltages which are of the same order of magnitude as the induced voltage.
Electromagnetic flowmeters are linear and have an excellent turndown of about 15:1. There is no practical size limit and no head loss. An insulated pipe section is required, with earth bonding either side of the metre to avoid damage from any welding which may occur in normal service. They can only be used on fluids with a conductivity in excess of 1 mS m–1, which permits use with many common liquids but excludes their use with gases.
Ultrasonic flowmeters
The Doppler effect occurs when there is relative motion between a sound transmitter and a receiver as shown in Fig. 4.17(a). If the transmitted frequency is ft, Vs is the speed of sound and v is the relative speed, the observed received frequency, fr is given by eqn 4.8.
A Doppler flowmeter injects an ultrasonic sound wave (typically a few hundred kilohertz) at an angle θ into a fluid moving in a pipe as shown in Fig. 4.17(b). A small part of this beam is reflected back from small bubbles and solid matter and is picked up by a receiver mounted alongside the transmitter. The frequency is subject to changes as it moves upstream against the flow and as it moves back with the flow. The received frequency is thus dependent on the flow velocity and the injection angle. As v is much smaller than Vs, the frequency shift is directly proportional to the flow velocity.
The Doppler flowmeter measures mean flow velocity, is linear, and can be installed or removed without the need to break into the pipe. The turndown of about 100:1 is
the best of all flowmeters. Assuming the measurement of mean flow velocity is accept- able it can be used at all Reynolds numbers.
Mass flowmeters
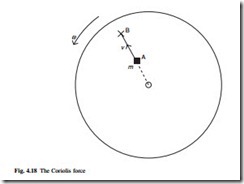
Many modern mass flowmeters are based on the Coriolis effect. In Fig. 4.18 an object of mass m is required to move with linear velocity v from point A to point B on a surface which is rotating with angular velocity ω. If the object moves in a straight line as viewed by a static observer, it will appear to veer to the right when viewed by an
observer on the disc. If the object is to move in a straight line as seen by an observer on the disc a force must be applied to the object as it moves out. This force is known as the Coriolis force and is given by
where m is the mass, ω is the angular velocity and v is the linear velocity.
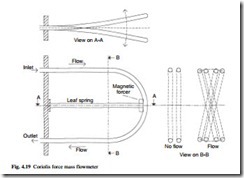
Coriolis force also occurs for sinusoidal motion. This effect is used as the basis of a Coriolis flowmeter shown in Fig. 4.19. The flow passes through a ‘C’ shaped tube which is attached to a leaf spring and vibrated sinusoidally by a magnetic forcer. The Coriolis force arises from the angular motion induced into the two horizontal pipe sections with respect to the fixed base. Any flow in the top pipe is in the opposite direction to the flow in the bottom pipe and the Coriolis force causes a rolling motion to be induced as shown. The resultant angular deflection is proportional to the mass flow rate.