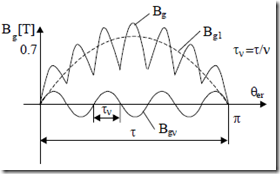
As already shown, the placement of coils in slots, the slot openings, and saturation cause airgap flux density harmonics (Figure 5.22).
The voltage (emf) induced in the stator and rotor phases (bars) is of paramount importance for the IM behavior. We will derive its general expression based on the flux per pole (Φν) for the ν harmonic (ν = 1 for the fundamental here; it is an “electrical” harmonic).
Φν = τνL Be gν (5.97)
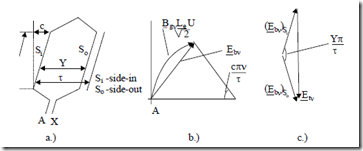
For low and medium power IMs, the rotor slots are skewed by a distance c (in meters here). Consequently, the phase angle of the airgap flux density along the inclined rotor (stator) slot varies continuously (Figure 5.23).
Figure 5.23 Chorded coil in skewed slots
a.) coil b.) emf per conductor c.) emf per turn
Consequently, the skewing factor Kskewν is (Figure 5.23b)
Kskew (5.98)
AOB τ ν 2
The emf induced in a bar (conductor) placed in a skewed slot Ebν (RMS) is
Ebν = 1 ω1Kskewν νΦ (5.99)
2 2
with ω1–the primary frequency (time harmonics are not considered here).
As a turn may have chorded throw (Figure 5.23a), the emfs in the two turn sides Si and So (in Figure 5.23c) are dephased by less than 1800. A vector composition is required and thus Etν is
Etν = 2K yνEbν; K yν = sinν (5.100)
Kyν is the chording factor.
There are nc turns per coil, so the coil emf Ecν is
Ecν = n Ec tν (5.101) In all there are q neighbouring coils per pole per phase. Let us consider them in series and with their emfs phase shifted by αecν = 2πp1ν/Ns (Figure 5.24). The resultant emf for the q coils (in series in our case) Ecν is
Ecν = qEcνKqν (5.102)
Kqν is called the distribution factor. For an integer q (Figure 5.24) Kqν is
Kq (5.103)
The total number of q coil groups is p1 (pole pairs) in single layer and 2p1 in double layer windings. Now we may introduce a≤p1 current paths in parallel.
The total number of turns/phase is W1 = p1qnc for single layer and, W1 = 2p1qnc for double layer windings, respectively. Per current path, we do have Wa turns.
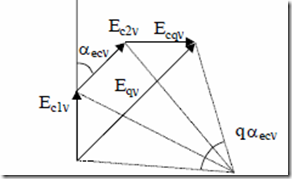
Figure 5.24 Distribution factor Kqν
Wa = Wa1 (5.104)
Consequently the emf per current path Ea is
Eaν = π 2f W K1 a qνK yνKcν νΦ (5.105)
For the stator phase emf, when the stator slots are straight, Kcν = 1.
For the emf induced in the rotor phase (bar) with inclined rotor slots, Kcν ≠ 1 and is calculated with (5.98).
(Eaν)stator = π 2f W K1 a sqνKsyνΦν (5.106)
(Ebν)rotor = π2 f K1 skewν νΦ (5.107)
(Eaν)rotor = π 2f W K1 a rqνKryνΦν (5.108)
The distribution Kqν and chording (Kyν) factors may differ in the wound rotor from stator.
Let us note that the distribution, chording, and skewing factors are identical to those derived for mmf harmonics. This is so because the source of airgap field distribution is the mmf distribution. The slot openings, or magnetic saturation influence on field harmonics is lumped into Φν.
The harmonic attenuation or cancellation through chording or skewing is also evident in (5.102) – (5.104). Harmonics that may be reduced or cancelled by chording or skewing are of the order
ν = Km ±1 (5.109)
For one of them
ν yτ π2 = K’ or π ν cτ π2 = K”π (5.110)
These are called mmf step (belt) harmonics (5, 7, 11, 13, 17, 19). Third mmf harmonics do not exist for star connection. However, as shown earlier, magnetic saturation may cause 3rd order harmonics, even 5th, 7th, 11th order harmonics, which may increase or decrease the corresponding mmf step harmonics. Even order harmonics may occur in two-phase windings or in three-phase windings with fractionary q. Finally, the slot harmonics orders νc are:
ν =c 2Kqm ±1 For fractionary q = a+b/c1, (5.111) ν =c 2(ac1 + b) K m ±1 (5.112)
We should notice that for all slot harmonics, Kqν = qsin 2sin 2[(( KqmKqm±±11))ππ/6/6q] = Kq1 (5.113)
Slot harmonics are related to slot openings presence or to the corresponding airgap permeance modulation. All slot harmonics have the same distribution factor with the fundamental, they may not be destroyed or reduced. However, as their amplitude (in airgap flux density) decreases with νc increasing, the only thing we may do is to increase their lowest order. Here the fractionary windings come into play (5.112). With q increased from 2 to 5/2, the lowest slot integer harmonic is increased (see (5.111) – (5.112)) from νcmin = 11 to νcmin = 29! (K/c1 = 2/2). As K is increased, the order ν of step (phase belt) harmonics (5.111) may become equal to νc.
Especially the first slot harmonics (K = 1, K/c1 = 1) may thus interact and amplify (or attenuate) the effect of mmf step harmonics of the same order. Intricate aspects like this will be dealt with in Chapter 10.