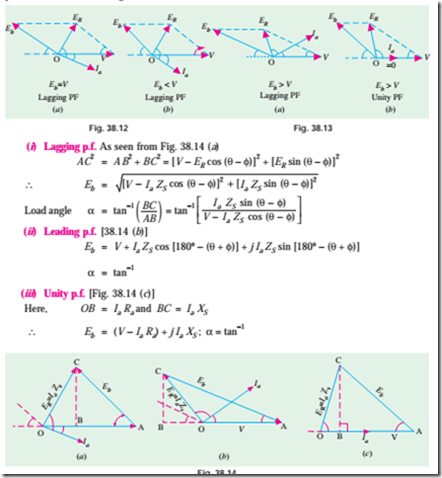
Synchronous Motor with Different Excitations
A synchronous motor is said to have normal excitation when its Eb = V . If field excitation is such that Eb < V , the motor is said to be under-excited. In both these conditions, it has a lagging power factor as shown in Fig. 38.12.
On the other hand, if d.c. field excitation is such that Eb > V , then motor is said to be over-excited and draws a leading current, as shown in Fig. 38.13 (a). There will be some value of excitation for which armature current will be in phase with V , so that power factor will become unity, as shown in Fig. 38.13 (b).
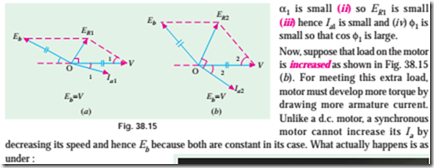
The value of a and back e.m.f. Eb can be found with the help of vector diagrams for various power factors, shown in Fig. 38.14.
Effect of Increased Load with Constant Excitation
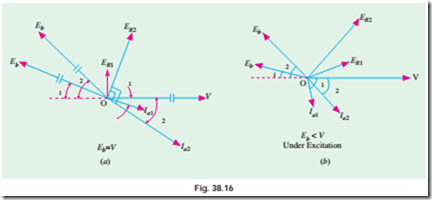
We will study the effect of increased load on a synchronous motor under conditions of normal, under and over-excitation (ignoring the effects of armature reaction). With normal excitation, Eb = V , with under excitation, Eb < V and with over-excitation, Eb > V . Whatever the value of excitation, it would be kept constant during our discussion. It would also be assumed that Ra is negligible as
compared to X S so that phase angle between ER and Ia i.e., q = 90º.
(i) Normal Excitation
Fig. 38.15. (a) shows the condition when motor is running with light load so that (i) torque angle
1. rotor falls back in phase i.e., load angle increases to a2 as shown in Fig. 38.15 (b),
2. the resultant voltage in armature is increased considerably to new value ER2,
3. as a result, Ia1 increases to Ia2, thereby increasing the torque developed by the motor,
4. f1 increases to f2, so that power factor decreases from cos f1 to the new value cos f2.
Since increase in Ia is much greater
than the slight decrease in power factor, the torque developed by the motor is increased (on the whole) to a new value sufficient to meet the extra load put on the motor. It will be seen that essentially it is by increasing its Ia that the motor is able to carry the extra load put on it.
A phase summary of the effect of increased load on a synchronous motor at normal excitation is shown in Fig. 38.16 (a) It is seen that there is a comparatively much greater increase in Ia than in f.
(ii) Under-excitation
As shown in Fig. 38.16 (b), with a small load and hence, small torque angle a1, Ia1 lags behind V by a large phase angle f1 which means poor power factor. Unlike normal excitation, a much larger armature current must flow for developing the same power because of poor power factor. That is why Ia1 of Fig. 38.16 (b) is larger than Ia1 of Fig. 38.15 (a).
As load increases, ER1 increases to ER2, consequently Ia1 increases to Ia2 and p.f. angle decreases from f1 to f2 or p.f. increases from cos f1 to cos f2. Due to increase both in Ia and p.f., power generated by the armature increases to meet the increased load. As seen, in this case, change in power factor is more than the change in Ia.
(iii) Over-excitation
When running on light load, a1 is small but Ia1 is comparatively larger and leads V by a larger angle f1. Like the under-excited motor, as more load is applied, the power factor improves and approaches unity. The armature current also increases thereby producing the necessary
increased armature power to meet the increased applied load (Fig. 38.17). However, it should be noted that in this case, power factor angle f decreases (or p.f. increases) at a faster rate than the armature current thereby producing the necessary increased power to meet the increased load applied to the motor.
Summary
The main points regarding the above three cases can be summarized as under :
1. As load on the motor increases, Ia increases regardless of excitation.
2. For under-and over-excited motors, p.f. tends to approach unity with increase in load.
3. Both with under-and over-excitation, change in p.f. is greater than in Ia with increase in load.
4. With normal excitation, when load is increased change in Ia is greater than in p.f. which tends to become increasingly lagging.
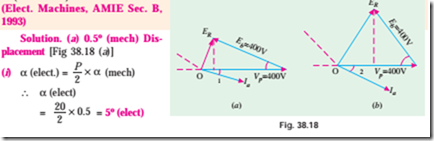
Example 38.2. A 20-pole, 693-V, 50-Hz, 3-f, D-connected synchronous motor is operating at no-load with normal excitation. It has armature ressistance per phase of zero and synchronous reactance of 10 W . If rotor is retarded by 0.5º (mechanical) from its synchronous position, compute.
(i) rotor displacement in electrical degrees
(ii) armature emf / phase
(iii) armature current / phase
(iv) power drawn by the motor
(v) power developed by armature
How will these quantities change when motor is loaded and the rotor displacement increases to 5º (mechanical) ?
1. rotor displacement increases from 5º (elect) to 50º (elect) i.e. Eb falls back in phase considerably.
2. ER increases from 35 V to 338 V/phase
3. Ia increases from 3.5 A to 33.8 A
4. angle f increases from 2.5º to 25.1º so that p.f. decreases from 0.999 (lag) to 0.906 (lag)
5. increase in power is almost directly proportional to increase in load angle. Obviously, increase in Ia is much more than decrease in power factor.
It is interesting to note that not only power but even Ia, ER and f also increase almost as many times as a.
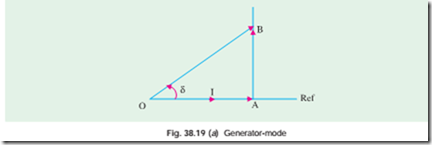
Special Illustrative Example 38.3 Case of Cylindrical Rotor Machine :
A 3-Phase synchronous machine is worked as follows: Generator – mode : 400 V/Ph, 32 A/Ph, Unity p.f. XS = 10 ohms. Motoring – mode : 400 V/Ph, 32 A/Ph, Unity p.f. , XS = 10 ohms. Calculate E and d in both the cases and comment.