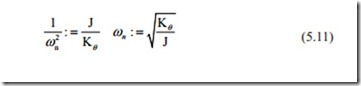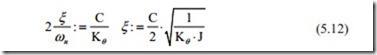Dynamic Response Characteristic over One Step Movement
It is important first to study the dynamic response of stepping motors for single step movement. To do this the linearized Eq. (5.4) must be used. In addition several assumptions have to be made. For the simplest model, the inductance of the windings is ignored. The voltage equation simply becomes
It can be seen that the governing transfer function in simplest form is a second order with two input variables of voltage and external torque. The coefficients of the characteristic equation gives the natural frequency and the damping ratio as
The natural frequency gives the speed of response and it can be seen that as the inertia increases the natural frequency reduces and as Kθ increases the natural frequency increases. The damping ratio is
If the mechanical damping coefficient C is zero, the rotor will oscillate continuous- ly. In practice, there is some mechanical friction that increases the damping ratio. It means that the rotor moves one step and will oscillate little and the teeth become aligned with the stator. Both Kθ and J reduce the damping ratio.
For a better mathematical model, the inductance of the stator windings must be taken into account. This only changes the voltage equation and the transfer function becomes third order which means that the motor might become unstable.