STEADY-STATE BY THE COMPLEX VARIABLE MODEL

By IM steady-state we mean constant speed and load. For a machine fed from a sinusoidal voltage symmetrical power grid, the phase voltages at IM terminals are

V_a,b,c = V 2 cos^{⋅ }ω −₁t (i−1)^{⋅ 2}3^{π }_; i =1,2,3 (13.39)

The voltage space phasor V_s^b in random coordinates (from (13.27)) is

For steady-state, the current in the space phasor model follows the voltage frequency: (ω₁ – ω_b). Steady-state in the state space equations means replacing d/dt with j(ω₁ – ω_b).

Using this observation makes Equations (13.30) become

Vs0 = R i_s s0 + ω Ψj ₁ s0; Ψ_s0 = L i_sl s0 + Ψ_m0;

Ψ_r0 = L i_rl r0 + Ψ_m0; im0 = is0 +ir0 (13.44)

= R i_r r0 + jSω Ψ₁ r0; S = (ω −ω¹_ωr ^r ); Ψ_m0 = L i_m m0 Vr0

So the form of space phasor model voltage equations under the steady-state is the same irrespective of the speed of the reference system ω_b.

When ω_b, only the frequency changes of voltages, currents, flux linkages in the space phasor model varies as it is ω₁ – ω_b.

No wonder this is so, as only Equations (13.44) exhibit the total emf, which should be independent of reference system speed ω_b. S is the slip, a variable well known by now. Notice that for ω_b = ω₁ (synchronous coordinates), d/dt = (ω₁ – ω_b) = 0. Consequently, for synchronous coordinates the steady-state means d.c. variables.

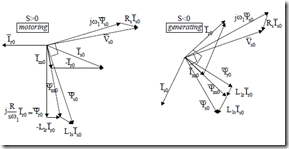
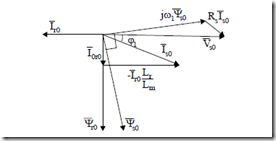
The space phasor diagram of (13.44) is shown in Figure 13.2 for a cage rotor IM.

cage rotor

Figure 13.2 Space phasor diagram for steady-state

From the stator space Equations (13.44) the torque (13.31) becomes

Te = 23 p1 jΨr0 r0i*  = 32 P1Ψr0 r0i (13.45) Also, from (13.44),

Ψ^r0 ir0 = −jSω₁ (13.46)

R_r With (13.46), alternatively, the torque is

T_e = 3 p1 Ψr02 Sω1 (13.47)

2 R_r

Solving for Ψ_r0 in Equations (13.44) lead to the standard torque formula.

3p1 Vs2 RSr

Te ≈ ω1 Rs +C1 RSr 2 +ω12 (Lls +C L1 lr )2 ; C1 = +1 LLmls (13.48)

Expression (13.47) shows that, for constant rotor flux space-phasor amplitude, the torque varies linearly with speed as it does in a separately excited d.c. motor. So all steady-state performance may be calculated using the spacephasor model as well.

EQUIVALENT CIRCUITS FOR DRIVES

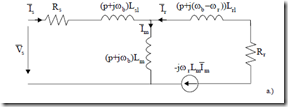
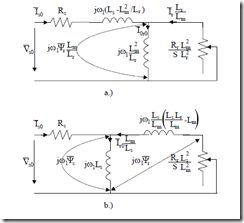
Equations (13.30) lead to a general equivalent circuit good for transients, especially in variable speed drives (Figure 13.3).

Vs = R is s +(p+ ωj b )L isls +(p+ ω Ψj b ) m (13.49)

Vr = R i_r r +(p+ j(ω −ω_{b r} ))L i_rl r +(p+ j(ω −ω_{b r} ))Ψ_m

The reference system speed ω_b may be random, but three particular values have met with rather wide acceptance.

• Stator coordinates: ω_b = 0; for steady-state: p Æ jω₁

• Rotor coordinates: ω_b = ω_r; for steady-state: p Æ jSω₁

• Synchronous coordinates: ω_b = ω₁; for steady-state: p Æ 0

Figure 13.3 The general equivalent circuit a.) and for steady-state b.) (continued)

Also, for steady-state in variable speed drives, the steady-state circuit, the same for all values of ω_b, comes from Figure 13.3a with p Æ j(ω₁ – ω_b) and Figure 13.3b.

Figure 13.3b shows, in fact, the standard T equivalent circuit of IM for steady-state, but in space phasors and not in phase phasors.

A general method to “arrange” the leakage inductances L_sl and L_rl in various positions in the equivalent circuit consists of a change of variables.

i^a_r = i /a; r Ψ_ma = aL_m^_is +i^a_r ^_ (13.50)

Making use of this change of variables in (13.49) yields

aVr = a R i²V^s_r =^ar +R i(^sp^s++j((ω −ωp _b+ ωj _br)()_{) (}La aL^s −aL_rl −^mL)_im^s ₎+i^a_r(_p++ ω Ψ(_pj+ ^bj()ω −ω_ba_{m r} ))_Ψ^a_m (13.51)

An equivalent circuit may be developed based on (13.51), Figure 13.4. The generalized equivalent circuit in Figure 13.4 warrants the following comments:

• For a = 1, the general equivalent circuit of Figure 13.4 is reobtained and

aΨ^a_m = Ψ_m : the main flux

• For a = L_m/L_r the inductance term in the “rotor section” “disappears”, being moved to the primary section and

aΨam = LLm_r Lmis +ir LLmr  = LLmr Ψr (13.52)

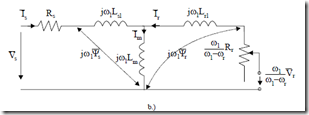
Figure 13.6 Steady-state equivalent circuits

a.) rotor flux oriented b.) stator flux oriented

• For a = L_s/L_m, the leakage inductance term is lumped into the “rotor section” and

aΨam = LLs Lm is +ir LLms  = Ψs (13.53)

m

• This type of equivalent circuit is adequate for stator flux orientation control

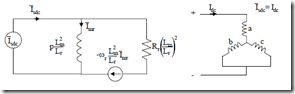
• For d.c. braking, the stator is fed with d.c. The method is used for variable speed drives. The model for this regime is obtained from Figure 13.4 by using a d.c. current source, ω_b = 0 (stator coordinates, V_r = 0, a = L_m/L_r) The result is shown in Figure 13.5.

For steady-state, the equivalent circuits for a_r = L_m/L_r and a_r = L_s/L_m and V_r=0 are shown in Figure 13.6.

Example 13.1. The constant rotor flux torque/speed curve.

Let us consider an induction motor with a single rotor cage and constant parameters: R_s = R_r = 1 Ω, L_sl = L_rl = 5 mH, L_m = 200 mH, Ψ_r0’ = 1 Wb, S = 0.2, ω₁ = 2π6 rad/s, p₁ = 2, V_r = 0. Find the torque, rotor current, stator current, stator and main flux and voltage for this situation. Draw the corresponding space phasor diagram.

Solution

We are going to use the equivalent circuit in Figure 13.6a and the rotor current and torque expressions (13.46 and 13.47):

T_e = ³ p₁ ^Ψr02 Sω =₁ ³ 2¹² 0.2 2 6⋅ π = 22.608Nm

2 R_r 2 1

Ψ^r0 = −0.2 2 6^{⋅ π 1} = −7.536A

I_r0 = − ωS ₁

R_r 1

The rotor current is placed along real axis in the negative direction. The rotor flux magnetization current Ir₀ (Figure 13.6a) is

I0r0 = −j(−Ir0 )LRSr₂LLmr = −j(−SωIr01L)Rm r = −j0.2 2 6 0.2 j5A

ω1 Lmr

The stator current

Is0 = −Ir0 ^Lr + I0_r0 = 7.536 ^0.205 − j5 = 7.7244− j5.0A

L_m 0.2

The stator flux Ψ_s is

Ψ_s0 = L I_s s0 + L I_m r0 = 0.205(7.7244− j5.0)+0.2(−7.536)= 0.076− j1.025 The airgap flux Ψ_m is

Ψ_m0 = L_m (Is0 + Ir0 )= 0.2 7.( 7244− j5.0−7.536)= 0.03768− j1.0

The rotor flux is

Ψ_r0 = Ψ_m0 + L I_rl r0 = 0.03768− j1.0+0.005(−7.536)= −j1.0 (as expected)

The voltage V_so is:

V_s0 = ω Ψj ₁ s0 + R I_s s0 = j2 6 0.π ( 076− j1.025)+1 7.( 7244− j5.0)= 46.346− j2.136 The corresponding space phasor diagram is shown in Figure A.