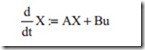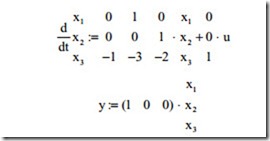State Variable Feedback Control Theory
It was shown in the previous chapter that control systems might have one or several outputs. The output is fed back in the controller and various control strategies may be used to control the system. The problem with complex system with higher order transfer function than third order is that it is not possible to control the location of the roots of characteristic equation on the s-plane. A compromise has to be made between the steady state error and the transient response.
In the state variable form, if all the state variables are measurable then state variable feedback control theory may be used. The condition is that the system must be controllable. The condition of controllability will be discussed later. If the state variables are not measurable for direct feedback, observer may be used to predict the state variables. The idea is that if the system model and input are known, with measurement taken on one or several state variables all state variables can be predicted. The condition of observability will be discussed later.
In the above equation, it is assumed that there is only one input variable. The pro- cedure for controllable system with more than one input is the same and it can be shown that by a single input it is possible to control the location of all roots of the characteristic equation. The control strategy is that a summation junction will be added to the input uiwhich represents the command signal and all state variables with appropriate gain are used as negative feedback. The state equation becomes
In Eq. (3.19), A is the system matrix, B is the input vector with dimension n × 1 which is a column vector and K is the gain vector with dimension 1 × n and X is the state variables. In Eq. (3.19) it should be possible to choose the gain so that the roots of characteristic equation are moved to the desired location on the s-plane. To do this first it is assumed that ui = 0 and the eigenvalue problem as discussed earlier will be studied. Without loss of generality, a third order transfer function will be considered. Suppose,
It should be noted that the operator s and derivative can be used interchangeably assuming that the initial conditions are zero.
The state equation with some algebraic manipulation becomes
Now the object is to choose a gain vector and all the state variables are fed back to the input summation junction. It would be interesting to the eigenvalues (roots of characteristic equation) of the open loop state equation. MathCad program software is used for this purpose as follows:
It can be seen that the open loop system is stable but the complex roots are un- derdamped. The gain vector must be selected such that to move all roots to de- sired position on s-plane. For this, the practical limitations such saturations, the limit of power amplifier, and nonlinearity of the system must be considered. Some practically achievable locations must be assumed for the eigenvalues. This can be achieved by trial and error strategy. A feedback strategy such as,
Therefore, the gain can be calculated with the above method. The gains become negative which shows that similar to the feedback control theory the state variables
are subtracted from the input signal. Although the control strategy was discussed for a third order transfer function, the method can be used for more complicated sys- tems. The eigenvalues of the system matrix with the state variable feedback control system can be calculated again to ensure the gains are correct.
The above analysis shows that indeed the eigenvalues have moved to the required position on the s-plane.
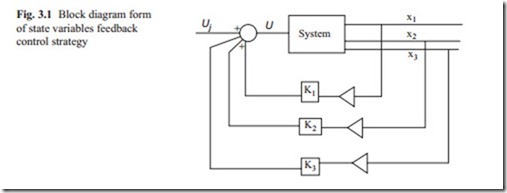
The control strategy mentioned above is shown in block diagram form in Fig. 3.1. When state variables feedback control system is used, it is important to study the steady state behavior of the system. For steady state, the derivative terms are set to
zero and the linear equation is solved as
It can be seen that there is a large steady state error. To overcome this problem, the roots must be moved away from the imaginary axis as far as possible or to use an integrator. When an integrator is added to the transfer function, the order of characteristic equation raises by one. This means that there will be four state variables and the system becomes more complicated. The reader is encouraged to study the above system with an integrator in the transfer function.