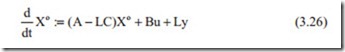Dynamic Observer
In state variables control theory, it is assumed that all state variables are measurable for direct feedback. If all state variables are not measurable or impractical, then state observer must be used. A dynamic observer is a computer program that by knowing the mathematical model of the system and input variables, calculates the estimate of the state variables. In principle, if the mathematical model and input variable is known, then it should be possible to solve the state equations to obtain the state variables. Therefore, for a state equation with system matrix A and input matrix B and input variable u, the observer equation becomes
In the above equation, the vector X0 represents the estimate of state variables. Other parameters have the usual meanings. The above equations can be solved numeri- cally by the method explained in the previous section assuming that the initial val- ues of X are known. In practice, the initial values may not be known and, therefore, a forcing function must be added to ensure that the estimates converge to the state variables of the system. First, it is useful to study the convergence of the error. The error is defined as the difference between the state variables and the observed state variables,where Xe are the errors.
Subtracting the observer state equation from the state equations and with some
algebraic manipulation gives
The only problem with the above equation is that the speed of response of the sys- tem matrix A is the same for the system and observer. Therefore, the observed variables cannot match that of the system. A forcing term must be added to the observer to ensure that the observed variables reach the state variables. This can be achieved by the following:
In Eq. (3.25), L is a constant matrix and for single output ( y) L is a vector. The term in the right hand side introduces a disturbance when the output differs by that of the observed output. C is the output matrix and again for a single output it is a vector. Writing Eq. (3.25) in slightly different forms gives
In Eq. (3.26), the matrix ( A − LC) is the new observer dynamic matrix and the val- ues of L must be chosen such that the observer dynamics is faster than that of the system. This means that the eigenvalues of observer must be chosen so that they are located to the left of the eigenvalues of the system. The design procedure is exactly the same as for selecting the gain vector K.
For very noisy output, the famous Kalman Filter or other form of estimator may be used which is beyond the scope of this book.
The observer in reality is a piece of software that performs numerical solution to the observer equation. This is the same as discussed in Eq. (3.18).
The above discussion is on full-order observer where all state variables are estimated. In some cases, a few state variables might be measurable and in this case a reduced-order observer might be used. Those who are interested in design of ob- server are referred to more advanced books. For servo control systems by some intelligent choices of state variables, they all can be measured directly from the system and use of observer must be avoided especially when there is significant noise in transducers.