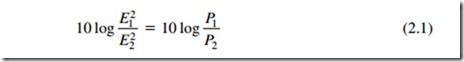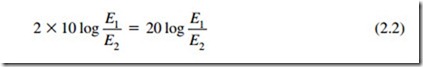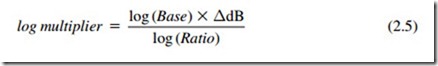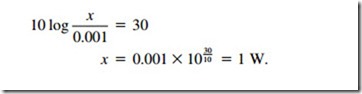Concepts Underlying the Decibel and its Use in Sound Systems
Most system measurements of level start with a voltage amplitude. Relative level changes at a given point can be observed on a voltmeter scale when it is realized that
which is only true if both values are measured at an identical point in their circuit. A common usage has been to remove the exponent from the ratio and apply it to the multiplier.
Bear in mind that the decibel is always and only based on a power ratio. Any other kind of ratio (i.e., voltage, current, or sound pressure) must first be turned into a power ratio by squaring and then converted into a power level in decibels.
Converting Voltage Ratios to Power Ratios
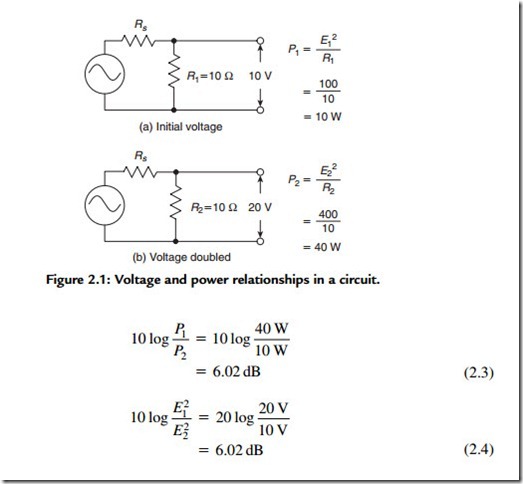
Many audio technicians are confused by the fact that doubling the voltage results in a 6-dB increase while doubling the power only results in a 3-dB increase. Figure 2.1
demonstrates what happens if we simultaneously check both the voltage and the power in a circuit where we double the voltage. Note that for a doubling of the voltage, the power increases four times.
One of the most common errors when using the decibel is to regard it as a voltage ratio (i.e., so many decibels above or below a reference voltage). To compound the error, the result is referred to as a “level.” The word “level” is reserved for power; an increase in the voltage magnitude is properly referred to as “amplification.”
However, the decibel can be legitimately used with a voltage reference. The reference is 1.0 V. When voltage magnitudes are referenced logarithmically, they are called dBV (i.e., dB above or below 1.0 V). This use is legitimate because all such measurements are made open circuit and can easily be converted into power levels at any impedance interface.
The following definition is from the IEEE Standard Dictionary of Electrical and Electronics Terms, Second Edition:
244.62
Voltage Amplification (1) (general). An increase in signal voltage magnitude in transmission from one point to another or the process thereof. See also: amplifier. 210 (2) (transducer). The scalar ratio of the signal output voltage to the signal input voltage.
Warning: By incorrect extension of the term decibel, this ratio is sometimes expressed in decibels by multiplying its common logarithm by 20. It may be currently expressed in decilogs. Note: If the input and/or output power consist of more than one component, such as multifrequency signal or noise, then the particular components used and their weighting must be specified. See also: Transducer.
239.210
Decilog (dg). A division of the logarithmic scale used for measuring the logarithm of the ratio of two values of any quantity. Note: Its value is such that the number of decilogs
is equal to 10 times the logarithm to the base 10 of the ratio. One decilog therefore corresponds to a ratio of 100.1 (that is 1.25829+).
The Decibel as a Power Ratio
Note that 20 W/10 W and 200 W/100 W both equal 3.01 dB, which means that a 2 to 1 (2:1) power ratio exists but reveals nothing about the actual powers. The human ear hears the same small difference between 1 and 2 W as it does between 100 and 200 W.
Changing decibels back to a power ratio (exponential form) is the same as for any logarithm with the addition of a multiplier (Figure 2.2). The arrows in Figure 2.2 indicate the transposition of quantities. Table 2.1 shows the number of decibels corresponding to various power ratios.
Finding Other Multipliers
Occasionally in acoustics, we may need multipliers other than 10 or 20. Once the ΔdB (the number of dB for a 2:1 ratio change) is known, calculate the multiplier by
The Decibel as a Power Quantity
We have seen that a number of decibels by themselves are only ratios. Given any reference (such as 50 W), we can use decibels to find absolute values. A standard reference for power in audio work is 10-3 W (0.001 W) or x V across Z Ω. Note that when a level is expressed as a wattage, it is not necessary to state an impedance, but when it is stated as a voltage, an impedance is mandatory. This power is called 0 dBm. The small “m” stands for milliwatt (0.001 W) or one-thousandth of a watt.
Example
The power in watts corresponding to +30 dBm is calculated as follows:
Note that this -12-dBm power level can appear across any impedance and will always be the same power level. Voltages will vary to maintain this power level. In constant- voltage systems the power level varies as the impedance is changed. In constant- current systems the voltage changes as the impedance varies