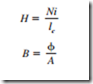MAGNETIC BEHAVIOR OF FERROMAGNETIC MATERIALS
The magnetic permeability is defined by the equation
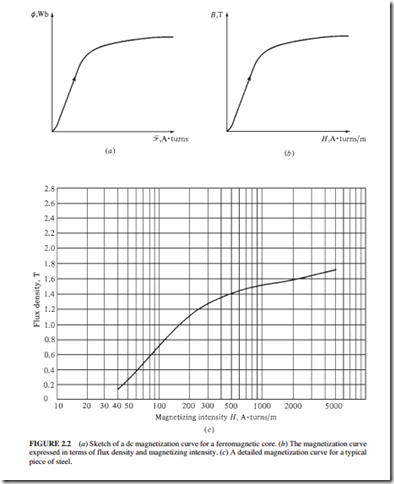
The permeability of ferromagnetic materials is up to 6000 times higher than the perme- ability of free space. However, the permeability of ferromagnetic materials is not constant. Suppose we apply a direct current to the core shown in Fig. 2.1 (starting with 0 A and increasing the current). Figure 2.2a illustrates the variation of the flux produced in the core versus the magnetomotive force. This graph is known as the saturation curve or magneti- zation curve. At first, a slight increase in the current (magnetomotive force) results in a sig- nificant increase in the flux. However, at a certain point, a further increase in current results in no change in the flux. The region where the curve is flat is called the saturation region. The core has become saturated. The region where the flux changes rapidly is called the unsaturated region. The transition region between the unsaturated region and the saturated region is called the knee of the curve.
Figure 2.2b illustrates the variation of magnetic flux density B with magnetizing inten- sity H. These are the equations:
It can easily be seen that the magnetizing intensity is directly proportional to the magneto- motive force, and the magnetic flux density is directly proportional to the flux. Therefore, the relationship between B and H has the same shape as the relationship between the flux and the magnetomotive force. The slope of flux-density versus the magnetizing intensity curve (Fig. 2.2c) is by definition the permeability of the core at that magnetizing intensity. The curve shows that in the unsaturated region the permeability is high and almost constant.
In the saturated region, the permeability drops to a very low value. Electric machines and transformers use ferromagnetic material for their cores because these materials produce much more flux than other materials.
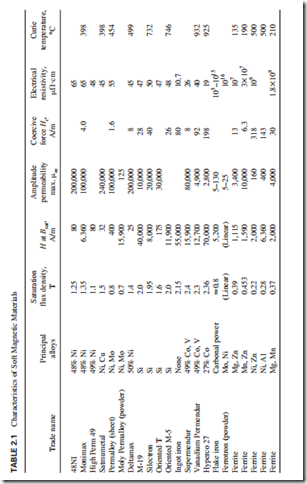
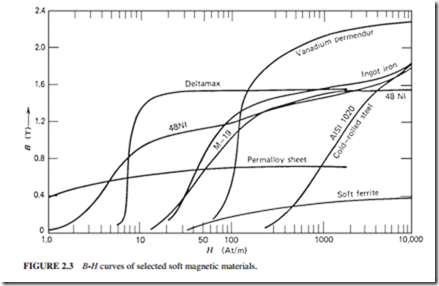
Table 2.1 lists the characteristics of soft magnetic materials including the Curie temperature (or Curie point) Tc. Above this temperature a ferromagnetic material becomes paramagnetic (weakly magnetized). Figure 2.3 shows several B–H curves of some soft magnetic materials.
Permalloy, supermendur, and other nickel alloys have a relative permeability greater than 105. Only a few materials have this high permeability over a limited range of operation. The highest permeability ratio of good and poor magnetic materials over a typical operating range is 104.
Energy Losses in a Ferromagnetic Core
If an alternating current (Fig. 2.4a) is applied to the core, the flux in the core will follow path ab (Fig. 2.4b). This graph is the saturation curve shown in Fig. 2.2. However, when the current drops, the flux follows a different path from the one it took when the current increased. When the current decreases, the flux follows path bcd. When the current increases again, the flux follows path bed.
The amount of flux present in the core depends on the history of the flux in the core and the magnitude of the current applied to the windings of the core. The dependence on the history of the preceding flux and the resulting failure to retrace the flux path is called hysteresis. Path bcdeb shown in Fig. 2.4 is called a hysteresis loop.
Notice that if a magnetomotive force is applied to the core and then removed, the flux will follow path abc. The flux does not return to zero when the magnetomotive force is removed. Instead, a magnetic field remains in the core. The magnetic field is known as the residual flux in the core. This is the technique used for producing permanent magnets. A magnetomotive force must be applied to the core in the opposite direction to return the flux to zero. This force is called the coercive magnetomotive force g;c.
To understand the cause of hysteresis, it is necessary to know the structure of the metal. There are many small regions within the metal called domains. The magnetic fields of all the atoms in each domain are pointing in the same direction. Thus, each domain within the metal acts as a small permanent magnet. These tiny domains are oriented randomly within the material. This is the reason that a piece of iron does not have a resultant flux (Fig. 2.5).
When an external magnetic field is applied to the block of iron, all the domains will line up in the direction of the field. This switching to align all the fields increases the magnetic flux in the iron. This is the reason why iron has a much higher permeability than air.
When all the atoms and domains of the iron line up with the external field, a further increase in the magnetomotive force will not be able to increase the flux. At this point, the iron has become saturated with flux. The core has reached the saturation region of the mag- netization curve (Fig. 2.2).
The cause of hysteresis is that when the external magnetic field is removed, the domains do not become completely random again. This is so because energy is required to turn the atoms in the domains. Originally, the external magnetic field provided energy to align the domains. When the field is removed, there is no source of energy to rotate the domains. The piece of iron has now become a permanent magnet.
Some of the domains will remain aligned until an external source of energy is supplied to change them. A large mechanical shock and heating are examples of external energy that can change the alignment of the domains. This is the reason why permanent magnets lose their magnetism when hit with a hammer or heated.
Energy is lost in all iron cores due to the fact that energy is required to turn the domains. The energy required to reorient the domains during each cycle of the alternating current is called the hysteresis loss in the iron core. The area enclosed in the hysteresis loop is directly proportional to the energy lost in a given ac cycle (Fig. 2.4).