INDUSTRIAL PROCESS CONTROLS
Definition and functions
Industrial processes in this context means those procedures in industries which involve chemical reactions, material changes, or mechanical steps which are carried out to effect the transport or manufacture of objects, usually on a very large scale.
There are many examples of industrial processes, including energy transmission, liquid flows, metal forges, chemical reactions, part cutting etc.
Industrial process control can be specified as the automatic monitoring and functioning of an industrial process, brought about by controllers or computers with programmed strategies and algorithms, associated with some devices and instruments to appropriately respond to feedback from the Advanced Industrial Control Technology.
process. Since the late twentieth century, the field of industrial process control has become increasingly important in chemical, pharmaceutical and petrochemical plants, oil refineries, energy trans- mission, and other related industries. This is because industrial process control can help industries to improve product quality, enhance production rates, stabilize plant and device operations, reduce working costs, minimize environmental pollution, etc. Advanced industrial process control in practise can be characterized as one or more of the following four types.
(1) Discrete process controls
Discrete industrial processes specify those industrial processes which handle distinct, separate products. In a discrete industrial process, both inputs and outputs must be discrete data flows and/or discrete data stores. Discrete processes can be found in many manufacturing, motion and packaging applications. The usual example is an automotive factory product line, where each car is a distinct artifact. Most discrete manufacturing involves the production of discrete pieces of product, such as metal stamping. Robotic assembly, such as that found in automotive production, can be characterized as discrete process control.
(2) Continuous process controls
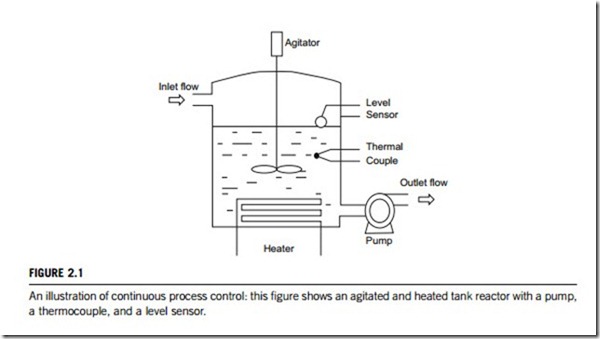
Some industrial processes are characterized by smooth and uninterrupted variables in time, and are defined as continuous processes. Some important continuous processes are the production of fuels, chemicals and plastics, forging, cutting, heating, etc. Continuous process control is commonly applied to these continuous processes. In a continuous process control system, the variables associated with any process are monitored and subsequent control actions are implemented to maintain variables within predetermined process constraints. Figure 2.1 is a simple continuous process control system.
(3) Batch process controls
In addition to discrete and continuous processes, there exists another industrial process known as the batch process. Batch processes are characterized by a prescribed processing of materials for a finite duration. This contrasts with continuous processes, where reactants are continually fed in, and products taken out. Batch industrial processes can be of two kinds; the first is the batch production process that leads to the production of specific quantities of product, by subjecting quantities of input materials to an ordered set of processing activities over a finite period using one or more pieces of equipment; the second is the batch chemical process in which a measured quantity of reactants is added to a reaction vessel, the reaction is carried out, and the products are then removed. Batch process control plays an important role in the chemical industry where low-volume, high-value products are required. Examples include reactors, crystallizers, injection molding processes, and the manufacture of polymers. Temperature and pressure profiles are implemented with servo-controllers, and precise sequencing operations are produced with tools such as programmable logic controllers (PLC).
(4) Statistical process controls
Statistical process control (SPC) is a control method for monitoring an industrial process through the use of a control chart. Much of its power lies in its ability to monitor both the process center and its variation about that center. By collecting data from samples at various temporal and spatial points within the process, variations in the process that may affect the quality of the end product or service can be detected and corrected, thus reducing waste and the likelihood that problems will be passed on to the customer. Process cycle-time reductions, coupled with improvements in yield, have made statistical process control a valuable tool from both a cost reduction and a customer satisfaction standpoint. With its emphasis on early detection and prevention of problems, statistical process control has a distinct advantage over quality methods, such as inspection, that apply resources to detecting and correcting problems in the end product or service. In addition to reducing waste, statistical process control can lead to a reduction in the time needed to produce the product or service from end to end. This is partly because the final product is less likely to need rework, but it also results from using statistical process control data to identify bottlenecks, wait times, and other sources of delays within the process.
Process variables
Flow, pressure, temperature and level are the four most common process variables. The control of these embodies many of the difficulties existing in all major process industries. Based on core process technology, worldwide process industries have delivered control solutions for some of the most intractable control problems. In most cases, there exists some general-purpose controller that can be used across industries to control a process variable directly without the need for system redesign (plug- and-play).
In this subsection, we present control solutions relating to temperature, pressure, flow, and level process controls with roadmaps for selecting appropriate controllers for specific control problems.
(1) Flow process control
Of the four variables mentioned flow is probably the least difficult to control but has the largest number of loops above, because it is a continuous process moving material from the beginning of the process to its end. Typically, the flow loop is controlled by manipulating valves, a variable frequency drive (VFD), or a pump.
A flow loop is naturally a first-order non-linear process with a small delay time. Since flow loops are the foundation of a process control system (for instance, they are typically used as the inner loop of a cascade control system), control of their performance is critical. How quickly the process variable stabilizes, whether there is an overshoot, how fast the overshoot damps out, and how fast the process variable can settle within a desired range are all quality criteria for the flow loop. In addition, inevitable wear and tear on the actuator can increase non-linearity in behavior. Therefore, the challenge for flow control is how to control a nonlinear process with stringent control performance requirements.
In flow process control, the commonly used actuators are nonlinear components by nature, including:
(a) a control valve, which is almost never a linear component; it can have a concave, convex, or square-shaped nonlinear relationship between its input and output; some of them even have hysteresis behavior that makes the problem much worse;
(b) a variable-frequency drive (VFD), which saves energy but is naturally a nonlinear device;
(c) a flow pump driven by a pulse-width modulator (PWM) based on the duty cycles, which does not necessarily have a linear relationship with the flow.
An example of flow process control is a gas-mixing process. For instance, if an iron and steel complex, operating units including blast furnaces, oxygen furnaces, and coking ovens all produce gases as by-products. Many plants discharge these gases into the atmosphere, wasting valuable energy and causing severe air pollution. A gas plant mixes these gases to produce fuel for the furnaces in metal casting and rolling mills. The quality of the mixed gas is measured by its heating value. Gases with inconsistent heating value can cause major control, quality, and production problems due to over- or under-heating. Even during normal production, gas supply and demand can change randomly. Major operating units such as blast furnaces and reheating furnaces may go online and offline periodically, causing huge disturbances in gas flow, pressure and the heating value. Online heating value analyzers are available, but are not usually used during normal operations, as they are difficult to maintain and overly expensive. Flow process control is applied to this gas-mixing process to monitor and control the gas heating value automatically in all operating conditions. For this purpose, a turnkey solution is used for heating value measurement and control. Using special, soft-sensor technology, the heating value can be accurately calculated online. An offline heating value analyzer can be used to calibrate the calculated value. Using model-free adaptive (MFA) controllers, gas flow and differential pressure loops can be effectively controlled. Robust MFA controllers are also used to handle the constraints and protect the system from running in vicious cycles. An MFA controller is used to control the gas heating value by cascading the gas flow and pressure controllers.
(2) Pressure process control
Pressure is another key process variable since its level is critical for boiling, chemical reaction, distillation, extrusion, vacuuming, and air conditioning. Poor pressure control can cause major safety, quality, and productivity problems. Overly high pressure inside a sealed vessel can cause an explo- sion. Therefore, it is highly desirable to keep pressure well controlled and maintained within safety limits. There are a number of reasons why a pressure loop is difficult to control, including the following.
(a) A pressure loop is nonlinear, thus a propotional-integrate-differentiate (PID) or model-based controller may work well in its linear range, but fail in its nonlinear rage. A natural gas pipeline and a fluidized-bed boiler are two examples of such a pressure loop.
(b) The pressure process is a multivariable process that cannot be efficiently controlled by using
single-input-single-output controllers due to interactions among the variables. For example, multiple gas pipelines may draw gas from a master pipeline. Therefore, when the load changes, these pipelines will interact with each other.
(c) Some pressure processes can generate high-speed and open-loop oscillations due to the poor frequency domain behavior of this process. For example, the pressure field and Mach speed value of an ultrasonic wind-tunnel, widely used in aerospace simulations, is open-loop oscillating. In this simulation experiment, it is very difficult to get an open-loop oscillation under control.
(d) The pressure process often involves large and varying time-delays. For example, pressure in
municipal gas grids or a product powder transport system has large and varying time delays. Unfortunately, a PID controller cannot effectively control a process with large and varying time delays so more complex solutions must be sought.
(e) Pressure loops are typically noisy; in other words the measured pressure may jump up and down
due to the nature of the pressure loop and the pressure sensor used.
In applications, use of model-free adaptive (MFA) controllers can help us to deal with some problems in pressure process control. Nonlinear MFA controllers can control nonlinear processes with no nonlinear characterization required. Robust MFA forces the pressure to stay inside the desired boundary of nonlinear control. The interactions between multivariable zones can be decoupled, by means of multiple-input multiple-output MFA control strategies, or algorithms, or feedback and feedforward MFA controllers. After choosing a phase-angle during configuration with a high-speed flex-phase MFA controller or a nonlinear flex-phase MFA controller, the flex-phase MFA can effec- tively control processes with bad behavior in the frequency domain. Furthermore, anti-delay MFA can effectively control processes with large time delays. Time-varying MFA can control processes with large and varying time delays. Low-pass filters can be used to screen the high-frequency noise. Since the MFA controller is not noise-sensitive, a filter may not be required unless the signal-to-noise ratio is so high that the control performance is obviously affected. Since the pressure loop requires fast sample and control update rates, the personal computer (PC)-based MFA control system may not be fast enough to control pressure loops. Embedded MFA control products or dedicated I/O cards in the PC will provide sufficient sample rates for pressure control. All embedded MFA control products can be used for pressure control. Some MFA control products have a user-entry field to pinpoint when the process variable is noisy. Based on the core MFA control method, various controllers have been developed to solve specific control problems.
A typical example of a pressure process is an onshore or offshore three-phase oil separator train, consisting of two separator vessels, with or without a slug catcher. Crude oil consisting of water, oil, and gas is separated by the system. Each vessel is typically controlled as a standalone unit. There are instances where a trip due to high pressure has occurred in one of the vessels while there is still spare capacity in another. Also, the gas pressure loop is nonlinear in nature and a random pulse of high pressure can cause the pressure loop to swing, resulting in frequent ignition of excess gas. This is a combined control and optimization problem, requiring an effective solution in order to control critical level and pressure loops and maximizing the separation capacity. A multiple-input multiple- output MFA controller is used to control the oil levels in a multivariable fashion. It can coordinate the related oil levels by simultaneously manipulating the related valves to prevent too high an oil level in one vessel while there is still storage room in others. This special MFA can balance the oil levels for both vessels, and so maximize usage of the vessel capacity. Since no process models are needed, commissioning and maintenance of the system is simple, with guaranteed performance. In another aspect, nonlinear MFA controllers are used for pressure loops. They easily configured to deal with gas loop nonlinearity and slug problems since nonlinear characterization is not required.
(3) Temperature process control
Temperature is important in industrial processes because it its value is critical for combustion, chemical reaction, fermentation, drying, calcination, distillation, concentration, extrusion, crystalli- zation, and air conditioning. Poor temperature control can cause major safety, quality, and productivity problems but it can be difficult to control in some applications. The many reasons why temperature is difficult to control are described in the following.
(a) Most temperature processes are very nonlinear because the dead band and slip-stick action of all the control valves make the temperature loop nonlinear. This means a PID or model-based controller may work well in its linear range and fail in its nonlinear range. Temperature processes are always looped at high speed due to ramping temperature up and down across a wide range at high speed. This is especially serious in the case of rapid thermal processing units for wafer treatment or for thermal testing of materials.
(b) In industry, it is often much faster to add heat to an operating unit than to take the heat away, if cooling is not available. Thus, the time constant can vary dramatically depending on whether the temperature is going up or down. Temperature processes are therefore slow and often time- varying. Varying time delays and time constants can easily cause a PID to oscillate or become sluggish. The PID can be tuned for certain operating conditions, but may fail when the process dynamics change.
(c) When subjected to large load changes and large inflow changes, temperature processes often deviate from normal. For example, steam generators in co-generation plants have to deal with large steam load fluctuations due to variations in steam users’ operating conditions; e.g. tomato hot-breaks for tomato paste production: tomatoes are dumped in by the truck-load, causing significant inflow variations. For large load changes, if the load doubles, it requires twice the amount of heat to maintain the temperature. Feedforward control is often required. For large inflow changes, if the inflow is solid, it is difficult to measure the flow rate; so feedforward control is not a viable solution.
(d) Some temperature processes are multiple-input single-output processes; however, some temperature processes are single-input multiple-output processes. For example, an air-handling unit of a building control system manipulates the heating valve, the cooling valve, and the damper, based on split-range control. This is a multiple-input single-output process. In distillation columns, both the bottom temperature and the tray temperature need to be controlled, but the reboiler steam flow is the only manipulated variable. It forms a single-input multiple-output process. In such a process, one controller has to deal with multiple processes such as heating and cooling. A fixed controller like a PID needs to be re-tuned when the control mode changes. In a single-input multiple-output process, the controller has only one variable to manipulate, but needs to control or maintain two or more process variables. In such cases, single-loop controllers such as a PID are not sufficient.
Based on the core MFA control method, various MFA controllers have been developed to solve specific control problems involving temperature. Without having to build on-line or off-line process models, an appropriate MFA controller can be selected and configured to control a complex temperature loop. MFA provides easy and effective solutions for previously intractable temperature control problems.
An example of temperature process control is the MFA control of multi-zone temperature loops. For instance, in a delayed coking process temperature loops can be controlled in multiple zones. In this control system, a cooker consists of two coking furnaces, each having two combustion chambers. High temperatures create carbon that clogs pipes, and a below-specified temperature causes an insufficient reaction so that the yield drops. Control difficulties result from large time delays; serious coupling between loops because the separation wall between the two chambers is quite low; multiple disturbances in gas pressure, oil flow rate, oil inflow temperature and oil composition. The oil outlet temperature is sensitive to gas flow rate change, and the temperature specification is tight (±1oC). An MFA control system running on a PC was networked to the existing distributed control system. The original cascade control design was simplified to eliminate disturbances and uncertainties. The new system regulates fuel flow directly to control the oil outlet temperature. A 2×2 anti-delay MFA controller on each furnace solves the large time delay and coupling problems. MFA controllers compensate for disturbances and uncertainties. Constraints on controller outputs prevent temperatures running too high or too low.
(4) Level process control
In process industries, the importance of level control is often overlooked. Typically, levels are controlled by manipulating the inflow or outflow to or from the operating unit, and it is considered to be an easy loop to control. Actually, it is difficult to tune a PID controller to give good control performance under all conditions, due to potential inflow and outflow variations of the operating unit. Overly tight level control will result in too much movement of the flow loop, which can cause excessive disturbances to the downstream operating unit. Thus, the PID level controller is usually detuned to allow the level process to fluctuate; so the variations of the outflow are minimized. The detuned PID, however, cannot provide rapid control of large disturbances, which may result in safety problems during a plant upset. In addition, oscillations in level during a process can cause the process to swing, which also results in a lower yield. Robust MFA controllers have been used to control level processes, which result in smooth material and energy transfers between the operating units, and also protect the levels from overflowing or becoming too dry during abnormal conditions.
To be successfully used for level control, a robust MFA controller must be configured in advance, considering the following configuration parameters:
(a) Upper and lower bound
These are the bounds within which the process variable is to be kept. These are “intelligent” upper and lower boundaries which typically are the marginal values which the process variable should not exceed. The process variable is unlike the controller output where a hard limit or constraint can be set. The process variable can only be changed by manipulating the output. Thus, the upper and lower bounds for the process variable are very different from the output constraints.
(b) Gain ratio
This is coefficient ratio that indicates how much the process variable should be multiplied by to determine the level of MFA action. A value of three is common in which case, as the process variable approaches its bounds, the MFA will treat as if it had received a value three times the actual. Notice that this is not a gain scheduling approach, although it appears to be. Gain scheduling is not able to resolve the complex problems described.
Based on the core MFA control method, various MFA controllers have been developed to solve specific control problems. This method applies to level process control as well. The robust MFA controller is well suited to control conventional level loops and provides good protection from running too high or too low.
Multi-input multi-output MFA can control the density and level for operating units such as evaporators. Two examples are introduced below to illustrate how to control level processes:
(a) Boiler steam drum level process control
The level of steam in the drum needs to be kept near a middle value to prevent either heat stress on the boiler water tubes (level too low) or corrosion (level too high). Improper control of the level can cause system shutdown, waste of energy, and shorter equipment life. Key variables affecting the steam level are feed water inflow, steam outflow and fuel/mixed inflow. Each variable has its own distinctive type of disturbance. Cold feed water creates a time delay in the process. A sudden increase in steam outflow causes a distinctive shrink and swell response. This will confuse the controller because the process will act in a different manner temporarily. A three-element MFA control system can effectively control the steam level. The MFA level controller is cascaded with the feed-water controller to regulate the level, and compensate for disturbances from feed water and steam outflow. The anti-delay MFA controller handles the widely varying delay time. Feedforward MFA controllers keep the feed water supply in balance.
(b) Evaporator level process control
Evaporators are operating units for dewatering, concentration, and crystallization processes in various industries. If the density or the consistency of the product is an important quality factor, the level process control will be much more difficult. For instance, tomato processing plants use evaporators to produce tomato paste. The density of the tomato paste is the most critical quality variable which needs to be controlled within a small range. The variables that can be manipulated are the inflow and outflow, which affect both density and fluid level at the same time. The evaporator, by its nature, is a multi-input multi-output process. When using single-loop controllers to control the level and density separately, both loops can oppose each other, causing major problems. A multivariable MFA controller can control density and level, quickly and tightly by manipulating inflow and outflow simultaneously. An MFA constraint controller protects the evaporator level from running too high or too low.
Control methodologies
Industrial process control strategies are used for controlling a process variable that fluctuates around a set point. The industrial process controller has a differentiator which determines a difference signal between a process variable and a set point. The subsection below will very briefly introduce several advanced process control methods for dealing with such situations of including open and closed loops, adaptive control, PID control, robust control, predictive control, and optimum control methods.
(1) Open and closed loops
Although open loop and closed loop are important methods of process control, the two terms are often not clearly distinguished. The differences between open-loop control and closed-loop are demonstrated in the following two examples; of a computer numerical control (CNC) system and a room temperature control system.
(a) CNC systems
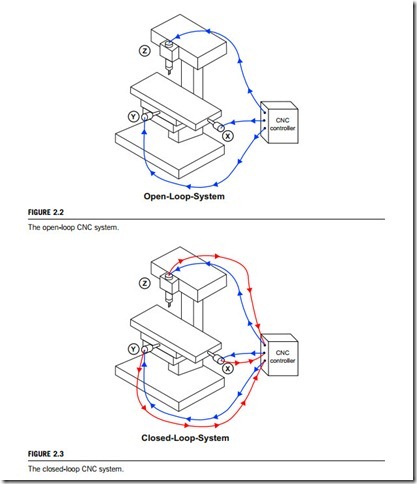
A CNC system requires motor drives to control both the position and the velocity of machine axes. Each axis must be driven separately, and must follow the command signal generated by the numerical control. There are two ways to activate the servo drives; the open-loop system and the closed-loop system.
In an open-loop CNC system, programmed instructions are fed into the controller through an input device. These instructions are then converted to electrical signals by the controller and sent to the servo amplifier to drive the servo motors. The cumulative number of electrical pulses determines the distance each servo drive will move, and the signal frequency determines the velocity of movement. The primary characteristic of the open-loop system is that there is no feedback system to check whether the desired position and velocity has been achieved. If system performance has been affected by load, temperature, humidity, or lubrication, then the actual output could deviate from that desired. For these reasons, the open-loop CNC system is generally used in point-to-point systems where accuracy is not critical. Very few, if any, continuous-path systems utilize open-loop control. Figure 2.2 illustrates the control mechanism of an open-loop CNC system.
The closed-loop CNC system has a feedback subsystem to monitor the actual output and correct any discrepancy from the programmed input. This can be either analog or digital. Analog systems measure the variation of physical variables, such as position and velocity, as voltages. Digital systems monitor output variations by means of electrical pulses. Closed-loop systems are very powerful and accurate because they are capable of monitoring operating conditions through feedback subsystems and can compensate for any variations automatically in real time. Most modern closed-loop CNC systems are able to provide very close resolution of 0.0001 of an inch. Closed-looped systems would, naturally, require more control devices and circuitry in order to implement both position and velocity control. This makes them more complex and more expensive than open-loop systems. A closed-loop CNC system is shown in Figure 2.3.
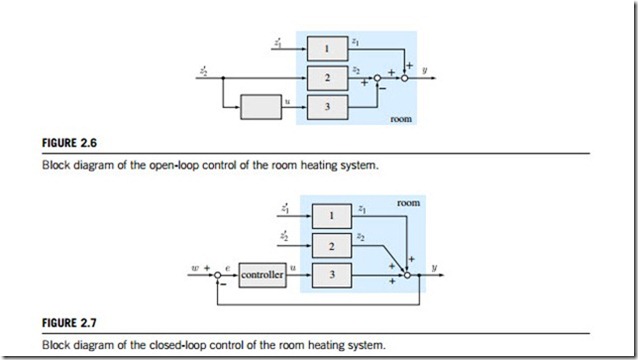
(b) A room heating system
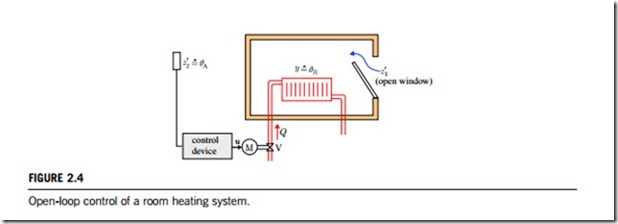
In the case of open-loop control of the room temperature (qR) according to Figure 2.4, the outdoor temperature (qA) will be measured by a temperature sensor and fed into a control device. In the case of
changes in the outdoor temperature qA (¼ disturbance z02) the control device adjusts the heating flow Q according to a slope function given by Q ¼ f (qA) using the motor M and the valve V. The slope given by this function can be tuned in the control device. If the room temperature qR is changed by opening a window (¼ disturbance z01), this will not influence the position of the valve, because only the outdoor temperature will influence the heating flow. Hence, this control principle will not compensate for the effects of all disturbances.
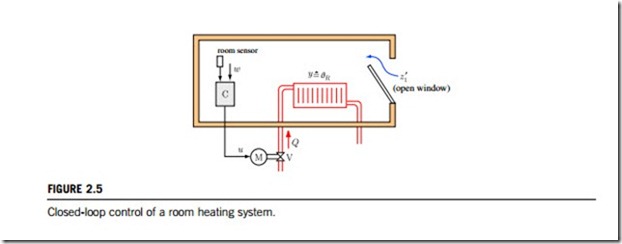
In the case of closed-loop control of the room temperature, as shown in Figure 2.5, the room temperature qR is measured and compared with a set-point value u, (for example, u ¼ 20oC). If the room temperature deviates from the given set-point value, a controller indicated by C alters the heat flow Q. All changes of the room temperature qR, including those that are for example, caused by opening the window or by solar radiation, are detected by the controller and compensated for.
Block diagrams of open-loop and closed-loop temperature control systems are shown in Figures2.6 and 2.7, and show the difference between the two control types very clearly. To this point, we can define systems in which the output quantity has no effect upon the process input quantity as open-loop control systems, and systems in which the output affects the process input quantity in such a manner as to maintain the desired output value are called closed-loop control system.
(2) Adaptive control
An adaptive control system can be defined as a feedback control system intelligent enough to adjust its characteristics in a changing environment so that some specified criteria are satisfied. Generally speaking, adaptive control methods are mainly suitable for (a) mechanical systems that do not have significant time delays; and (b) systems that have been designed so that their dynamics are well understood.
Adaptive control methods, either model reference or self-tuning, usually require some kind of identification of the process dynamics. This contributes to a number of fundamental problems such as
(a) the amount of offline training required, (b) the trade-off between the persistent excitation of signals for correct identification and the steady system response for control performance, (c) the assumption of the process structure, and (d) the model convergence and system stability issues in real applications. In addition, traditional adaptive control methods assume knowledge of the process structure. They have major difficulties in dealing with nonlinear, structure-variant, or with large timedelays processes.
(3) PID control
Many industrial processes are still controlled manually, or by 60-year-old PID controllers. PID is a simple general-purpose automatic controller that is useful for controlling simple processes. However, PID has significant limitations:
(a) PID works in process that is basically linear and time-invariant; it cannot control effectively complex processes that are nonlinear, time-variant, coupled, or have large time delays, major disturbances, and uncertainties. PID is not adequate for industrial processes with changing fuels and operating conditions.
2.1 Industrial process controls 53
(b) PID parameters have to be tuned properly. If the process dynamics vary due to fuel changes or load changes, PID needs to be re-tuned. This is often a frustrating and time-consuming experience.
(c) PID is a fixed controller, which cannot be used as the core of a smart control system.
(4) Robust control
Robust control is a controller design method that focuses on the reliability (robustness) of the control algorithm. Robustness is usually defined as the minimum requirement a control system has to satisfy in order to be useful in a practical environment. Once the controller is designed, its parameters do not change and control performance is guaranteed. The design of a robust control system is typically based on the worst-case scenario, so that the system usually does not work at optimal status under normal circumstances.
Robust control methods are well suited to applications where system stability and reliability are top priorities, where process dynamics are known, and variation ranges for uncertainties can be estimated. Aircraft and spacecraft controls are some examples of these systems.
In process control applications, some control systems can be designed with robust control methods, especially for those processes that are mission-critical and have large uncertainty ranges, and small stability margins.
(5) Predictive control
Predictive control, or model predictive control (MPC), is one of only a few advanced control methods that are used successfully in industrial control applications. The essence of predictive control is based on three key elements; (a) a predictive model, (b) optimization in range of a temporal window, and (c) feedback correction. These three steps are usually carried continuously by online out programs.
Predictive control is a control algorithm based on a predictive model of the process. The model is
used to predict the future output based on historical information about the process, as well as antic- ipated future input. It emphasizes the function of the model, not the structure of the model. Therefore, a state equation, transfer function, or even a step or impulse response can be used as the predictive model. The predictive model is capable of showing the future behavior of the system. Therefore, the designer can experiment with different control laws to see the resulting system output, using computer simulation.
Predictive control is an algorithm of optimal control. It calculates future control action based on a penalty or a performance function. The optimization of predictive control is limited to a moving time interval and is carried on continuously on-line. The moving time interval is sometimes called a temporal window. This is the key difference from traditional optimal control, which uses a perfor- mance function to judge global optimization. This idea works well for complex systems with dynamic changes and uncertainties, since there is no reason in this case to judge optimization performance over the full time range.
(6) Optimum control
Optimal control is an important component of modern control theory. In principle, optimal control problems belong to the calculus of variations. Pontryagin’s maximum principle and Bellman’s dynamic programming are two powerful tools that are used to solve closed-set constrained variation problems, which are related to most optimal control problems. The statement of a typical optimal control problem can be expressed as follows: The state equation and initial condition of the system to be controlled are given. The objective set is also provided. Find a feasible control, such that the system that starts from the given initial condition transfers its state to the objective set, and in so doing minimizes a performance index.
In industrial systems, there are some situations where optimal control can be applied, such as the control of bacterial content in a bioengineering system. However, most process control problems are related to the control of flow, pressure, temperature, and level. They are not well suited to the application of optimal control techniques.
(7) Intelligent control
Intelligent control is another major field in modern control technology. There are different definitions regarding intelligent control, but it denotes a control paradigm that uses various artificial intelligence techniques, which may include the following methods: (a) learning control, (b) expert control, (c) fuzzy control, and (d) neural network control.