INDUSTRIAL MOTION CONTROLS
Motion control applications
In industry, there are many applications in which there is a need to command, control, and monitor the motion of those components, parts of machines, equipment, or systems. The desired motion profile of such devices must sometimes be changed either during normal operation, at set-up, or under emergency conditions. This is known as industrial motion control. Industrial motion control primarily delivers control functions for velocity, acceleration and deceleration, position or torque.
(1) Velocity control
Velocity, or speed control is a common motion control mechanism. Several aspects of the velocity behavior of the system to be controlled must be clarified at the outset. Firstly, what is the speed required to operate the application? Secondly, does load of this application vary with speed or is load constant?
For a typical robot, differential velocities are used for steering. For example, in order to go straight,both motor shafts have to be turning at precisely the same rate, and the wheels must also be the same diameter. In another example, a machine tool axis will require, in general, constant thrust over a fairly wide range of cutting speeds, plus have a high-speed requirement at low load for rapid traversing. This results in an overall speed range of two or three orders of magnitude. In contrast, a machine tool spindle that drives a part in a lathe, or tool for milling, will require fairly constant power over a speed range of perhaps 5 to 1 as supplied by the motor. This is because the transmissions are generally added to further extend the constant power range.
Another consideration of velocity control is speed regulation. Speed regulation is generally
expressed as percent of speed. Speed regulation may be short-term or long-term dependin on the application. Short-term regulation would be necessary for speed deviation due to some transient load of a known quantity. Long-term regulation would be needed for speed control over seconds, minutes, or longer. In addition, speed ripple in a system, often the result of motor and driver design, may be a concern at certain frequencies to which the application is sensitive. Examples of this would be the effects of speed ripple on the surface finish of parts made by machine tools, or on the coating consistency of metals in an optical plating process driven by motors.
(2) Acceleration and deceleration control
The acceleration and deceleration controls is a higher level operation than velocity control in motion control. The acceleration or deceleration rate will affect the forces in the system, since torque is the product of inertia and rate of changed speed. It is important to include the inertia of the actuator or motor in any force calculation of this kind because its inertia may contribute considerably to the torque required. The selection of acceleration or deceleration profiles will also affect control performance. Linear acceleration is needed for a motor to change smoothly from one velocity to the next until the target speed is achieved. However, acceleration that follows a non-linear, curved profile gives rates of change that vary with both position and velocity.
Curve-profiling is important in acceleration and deceleration control. S-curve acceleration has a low initial rate of change and then increases to a maximum rate, then decreases again until the target speed is achieved. A parabolic profile begins acceleration at a high rate, and then decreases. Braking a car to a stop at exactly the right spot is one example of deceleration control using a parabolic profile.
(3) Position control
Position control entails the control of motion of displacement, which is the change of position with respect to time. This includes command, control, and the monitoring of motion. This can be as simple as the change in velocity obtained by limit switches on a simple slide drive, or as complex as linear and circular interpolation among axes on a multi-axis machine. Position control typically needs to be able to change certain parameters of the required motion flexibly. For example, the length of the move or the speed of the system may change based on variables in the process, or the parts being manufactured. The resolution of the position control, i.e., the smallest unit of displacement, needs to be defined. Along with the resolution, the accuracy and repeatability of the motion displacement need to be determined. Resolution, accuracy, and repeatability are common performance measures associated with position feedback devices such as encoders and resolvers; but the specification of a complete motion system must also take into account the mechanical system and position controller.
Position control loops are performed by a user inputting a desired position and the servo logic drives the output shaft to that position with whatever force is required. Normally one does not think of position control as being appropriate for doing motion control on small robots, but, in fact, it is a very good technique. The trick is to profile a series of positions for the robot to be in, feeding that string of positions to the servo on a periodic basis. This is called position-profiling. With position-profiling the forward velocity of the robot can be any arbitrary low amount. It might be that the motor shafts advance only every so often, but they will advance smoothly and the robot will crawl along. With profiling, acceleration becomes easy to do as well.
(4) Torque control
Torque control is widely used as a method for controlling the torque or force in a system, indepen- dently to its speed. An example would be a simple feed or take-up tension control in making rolls. Maintaining constant tension by varying torque at the rolls as a function of roll diameter will certainly result in a constant power requirement. A more complex tension control might require a changing or tapered tension as a function of roll diameter. As in the evaluation of a velocity controlled system, a torque controlled system needs to be quantified by a number of parameters: what is the required torque range? Over what speed range must the torque be provided? Is torque ripple of concern, and, if so, what frequencies of ripple present a problem?
Torque control is a unique method for controlling AC motors. In pulse-width modulation drives, the output frequency and voltage are the primary control reference signals for the power switches, rather than the desired torque in and out of the motor shaft. The torque control principle can be illustrated via this mechanical analogy of the continuous calculation of the best angle at which to rotate a shaft, with a given arm length and the forces available. These electrical force vectors are generated with the help of semiconductor switches called integrated gate bipolar transistors (IGBT). Testing of rotating machines such as gears, engines, and complete cars is a demanding task. High accuracy and dynamic load control, that is, control of torque, are both needed for clutch transmissions being introduced into the current generation of automobiles. AC motors drive these test rigs. When manufacturing such test rigs, which have stringent performance requirements, careful consideration must be given to the AC machines and drives to be used (control of speed and torque are paramount). The way the AC motor is controlled by its drive has a primary effect on these considerations.
Advanced motion control
Advanced motion control requires two control mechanisms: servo and feedback. In most industrial applications, these two mechanisms are combined to perform servo-feedback functions for motion control.
(1) Servo control
The basic reasons for using servo systems in industrial motion control include the need to improve transient response times, to reduce steady-state errors, and to reduce the sensitivity to load parameters. Improving the transient response time generally means increasing the system bandwidth. Faster response times mean quicker settling, allowing for higher machine throughput. Reducing the steady- state errors relates to servo system accuracy. Finally, reducing the sensitivity to load parameters means the servo system can tolerate fluctuations in both input and output parameters.
Servo control in general can be broken down into two fundamental classes of problem. The first deals with command tracking i.e., how well the actual motion follows what is being commanded.
The second general class of servo control addresses the disturbance rejection characteristics of the system. The typical commands of rotary motion control are position, velocity, acceleration and torque. For linear motion, force is used instead of torque. The part of servo control that deals with this directly is often referred to as feedforward control. Feedforward control predicts the internal commands needed for zero errors.
The feed forward commands can be thought of as the internal commands that are needed such that the user’s motion commands are followed without any error, assuming of course that a sufficiently accurate model of both the motor and load. The disturbance rejection control reacts to unknown disturbances and modeling errors. Disturbances can be anything from torque disturbances on the motor shaft to incorrect motor parameter estimations used in the feedforward control. The familiar proportional-integral-derivative (PID) and proportional-integral-velocity (PIV) controls are used to combat these types of problems.
Complete servo control systems combine both feed forward and disturbance rejection control to optimize overall performance.
In a PID control system, the PID controller calculation involves three separate parameters; the proportional, the integral and the derivative values. The proportional value determines the reaction to the current error, the integral determines the reaction based on the sum of recent errors, and the derivative determines the reaction to the rate at which the error has been changing. The weighted sum of these three actions is used to adjust the process via a control element such as the position of a control valve, or the power supply of a heating element. By tuning the three constants in the PID controller algorithm, the PID can provide a control action designed for specific process requirements. The response of the controller can be described in terms of responsiveness to an error, the degree to which the it overshoots the set-point and the degree of system oscillation. Note that the use of the PID algorithm does not guarantee optimum control of the system, or system stability.
In contrast to the PID control, the PIV control requires knowledge of the motor velocity, labeled the velocity estimator. This is usually done by a simple filter, but significant delays can result, and must be dealt with if truly accurate responses are needed. Alternatively, the velocity can be obtained by use of a velocity observer. This observer uses other state variables in order to provide zero-lag filtering properties. In either case, a clean velocity signal must be provided for PIV control. To tune such a system, only two control parameters are needed the bandwidth and the damping ratio. An estimate of the motor’s total inertia and damping is also required at set-up, and is obtained using the motor/drive set up utilities.
(2) Feedback control
Feedback can be described as a function that transforms inputs to outputs, such as an amplifier that accepts a signal from a sensor and amplifies it, or a mechanical gearbox with an input and output shaft.
When analyzing such systems we will often use transform functions that describe a system as a ratio of output to input.
There are two main types of feedback control systems: negative and positive. In a positive feedback control system the set-point and output values are added. In a negative feedback control the set-point and output values are subtracted. As a rule negative feedback systems are more stable than positive feedback systems. Negative feedback also makes systems more immune to random variations in component values and inputs.
Motion control systems
A motion system can be very complex and may include many different types of motion components. An example of such a system is a computer integrated manufacturing (CIM) system which receives as input a computer-aided design (CAD) data file. It inspects and loads tools into a manufacturing cell, makes a part in accordance with the CAD information, provides real-time adjustment the manufacturing process, and then collects, processes, and stores information for statistical process control purposes. This system will include many types of motion control systems; controllers, amplifiers, motors and actuators, and feedback devices. The combination of these components required to perform a given application will vary, and many considerations affect which type of system is the best one.
Often two factors need to be considered in designing a motion control system.
(1) At the top of a motion control hierarchy is the profile generator, which will typically contain many defined profiles. When a specific profile is selected, the profile generator will feed its velocity and position commands to the next block, which is the real-time control loop of the drive.
(2) The drive module can include both velocity and torque control inner loops or not, depending on the control technique used. The output of this block is drive power to the motor, with feedback from the motor output providing position information (typically through encoders or resolvers) plus velocity information (with tachometers) for the drive loop.
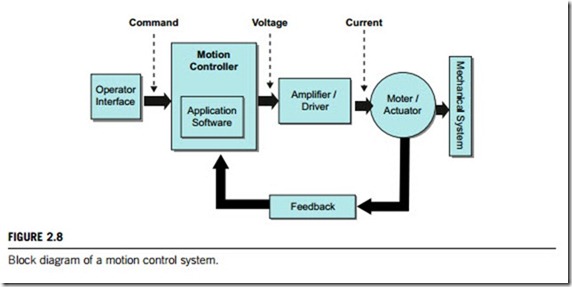
Figure 2.8 shows a block diagram of a typical motion control system that includes; the operator interface, usually a human machine interface (HMI) for communication between operator and controller; the motion controller, which acts as the brain of the system by taking the desired target positions and motion profiles, and creating the trajectories for the motors by outputting a voltage signal for motor or actuator to follow; application software, which gives target positions and motion control profiles commands; amplifiers (or drives), which take the commands in voltage signals from the controller and then generate the current required to drive or turn the motor; motors or actuators, which turn electrical energy into mechanical energy and produce the torque required to move to the desired target position; mechanical elements, which are designed to provide torque to some devices such as linear slides, robot arms, special actuators and so on; a feedback device, usually a quadrature encoder, which senses the motor position and reports the result back to the controller. A feedback function would not be required for some motion control applications such as controlling stepper motors, but is vital for servo motors.
Motion control technologies
Industrial motion control involves very complicated electronic and mechanical technologies. When implementing and testing a motion control system, we need to take account of many technical issues. The following lists some key issues for motion control technology.
(1) Repeatability and accuracy
It will involve a combination of art, science, and experience to choose the correct motion control components for a successful servo positioning system. Motion control systems typically employ
a combination of belts, ball screws, lead screws, and motors for determining speed, torque, and direction. All of these four components are contained in the motion controller.
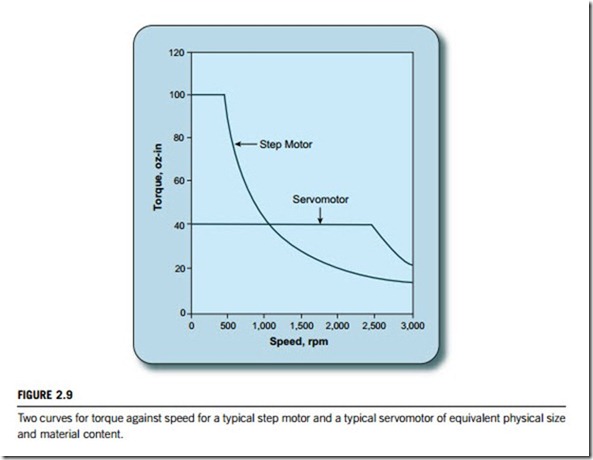
When selecting the components for a motion control system, the first factors to consider are speed and torque, which will determine whether the system should host a stepper motor or a servo motor. Steppers are usually superior for systems that operate at speeds lower than 1,000 rpm (rotations per minute) and less than 200 watts. By comparison, as shown in Figure 2.9, servomotors are preferred for speeds above 1,000 rpm and power levels above 200 watts. Each has a unique set of parameters that contribute to its accuracy, resolution, and repeatability.
The next issue for selecting motion system components concerns feedback devices. Steppers do not require feedback; servo motors use feedback devices by definition. Servo systems require one or more feedback signals in simple or complex configurations, depending on the specific needs of the motion system. Feedback loops record position, velocity or speed, acceleration and deceleration. Sometimes, feedback also includes “jerk”; the first derivative of acceleration with respect to time.
The motor amplifier or drive (as illustrated in Figure 2.8) is the part of the motion control system that takes commands from the motion controller, in the form of analog voltage signals of low current, and converts them into high current signals that drive the motor. Motor drives come in many different
varieties and are matched to a specific type of motor. For example, a stepper motor drive connects to stepper motors, and not servo motors. Along with matching the motor technology, the drive must also provide the correct peak current, continuous current, and voltage to drive the motor. If a drive supplies too much current, it could risk damaging motor. If a drive supplies too little current, the motor does not reach full torque capacity. If system’s voltage is too low, a motor cannot run at its full speed.
Motion control systems are usually specified to perform any one or a combination of three different types of moves. These include unidirectional, point-to-point bidirectional, and contouring modes. Unidirectional moves require point-to-point repeatable moves, in which the destination point is approached from only one direction. Accuracy for these systems is more difficult to achieve, as also serves as a measurement system. Highly repeatable unidirectional systems are usually also highly accurate. Bidirectional repeatability is more difficult to achieve because of backlash and hysteresis. Many motion controllers can compensate for repeatable gear backlash, but fail to handle other components with less predictable backlash. Supplying a secondary encoder for position information can compensate for backlash. Highly accurate and repeatable systems often use a position sensor outside the motor. Care must be taken with these systems since the hysteresis or dead-band would be enclosed within the position loop. Hysteresis is evident when the system is commanded to reach the same destination from opposite directions. A rotary encoder coupled to the motor would indicate that the load has reached its destination, but the actual position error is larger than the backlash alone. This hysteresis is caused by unseen clearances and elastic deformations. A linear encoder can compensate for backlash and hysteresis in a screw-driven positioning system. The hysteresis must still be mini- mized to avoid problems with oscillation, and systems with hysteresis potentials must minimized friction.
(2) Motor power transformation
In motion control systems, motors are the components that convert electrical power to useful mechanical power. Gearheads transform the mechanical rotary power to the desired combination of speed and torque if the motor cannot do so directly. Transmission systems are chosen on the basis of performance, size, cost, and various other constraints. Whilst each type of system has its own benefits and disadvantages, gearing systems hold many advantages for economic power consumption in small packages.
There are several types of electrical motors and power transmission devices. Depending on theapplication, a designer might first choose between alternating current (AC) and direct current (DC) motors, then between styles (including induction, universal, and permanent magnet), and finally between the many types specific to each style. The designer must also select a controlling device and amplifier to provide the proper input power for the motor. For example, the motor may be capable of supplying the necessary power, but not match the speed or torque requirements. Most motors are rated to operate for peak output around a certain continuous load range of torque and speed. To operate the motor outside that range would either under-utilize the motor and result in an oversized motor, or over- utilize the motor and potentially run the risk of damage motor. Although each type and style of motor operates differently, smaller motors typically operate more efficiently at higher speeds and lower torques. Larger motors operate at higher torques and lower speeds. This is obvious if the motor is viewed as a large moment arm.
High-energy, permanent magnet, servo motors have become extremely popular industrial motion controls. For these motors, a general rule of thumb is that if the length of the motor is doubled, then the output torque capacity of the motor is also doubled. However, the output torque capacity of the motor will be quadrupled if the length is kept the same and the diameter of the motor is doubled. For maximum efficiency, proper sizing, and economy, it is best to design the motor for operation at, or slightly under, its designed load point of speed and torque.
The speed-reducing planetary gearhead as described adheres to the following:
ratio ¼ (Ns þ Nr)/Ns (where Ns ¼ number of sun gear teeth and Nr ¼ number of ring gear teeth). There are many variations of epicycle gearing that can be produced from this style. In some instances, the ring gear can be the driving gear or the output gear. Complex epicycle, or planetary gearing is also possible, in which gear clusters are used in planetary configurations. An automobile transmission is a good example of how several styles of planetary gearing can be utilized together.
To enhance the output of such a spur gear design, a style of involuted spur gearing, known as epicycle gearing (i.e., planetary gearing), was developed. Planetary gearing dramatically increased the strength of the gearhead while eliminating radial loading, by counterbalancing the effect of any one- gear engagement. Planetary gearheads distribute the input power coming from the sun gear (input pinion) to two or more planetary gears. Since the planet gears are positioned symmetrical to the pinion gear, radial loading on the pinion gear is eliminated. The planet gears are housed within a ring gear, which has gear teeth cut into the inside diameter in a reversed tooth profile. The separating forces (radial forces) produced from the planet gears’ tooth engagement with the sun and ring gears cancel each other. The ring gear is stationary, and the input sun gear pinion drives the planet gears, which then walk in the same rotational direction as the sun gear.
Depending on the number of teeth in the sun gear and ring gear, each stage typically generates speed reduction ratios of between 3 and 10 times the input speed. A two-stage planetary gearhead, which has two 10-to-1 stages (i.e., 10 rotations of the input pinion results in one rotation of the output), yields 100 times the output torque (less efficiency) and 1/100 the rpm. If the gearhead were reversed so that the output shaft becomes the input shaft, the speed would increase by 100 times; the available output torque would decrease proportionately.