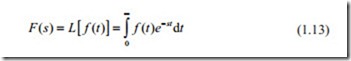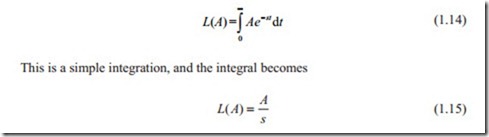Laplace Transform
By the definition, the Laplace Transform is defined as
By taking the Laplace Transform, the variable t is eliminated and the result is only function of s.
Equation (1.13) appears to be very complicated, and indeed for complicated transformation, the integral becomes very complex. Fortunately, for control systems only a few functions are needed.
The transformation of some common functions that are used in control are shown in Table 1.1. There are a few important Laplace Transform that are often used in defining performance of servo control systems. These are constant values which
represent step input; the ramp and acceleration inputs are other parameters that are often used in analysis to determine the performance.
The above table gives the Laplace Transform of the most useful function. Also note that the Laplace Transform is the only function of s only. This enables us to treat differential equation like algebraic function. Some examples will clarify this point, and they show how differential equation is converted to s domain and how the solution can be obtained from the Laplace Transform.
Example 3 Speed of DC motors assuming negligible inductance.
In this example, only a brief discussion on modeling of DC motors will be given. Full details of analysis will be discussed in a different chapter.
The voltage equation can be written as
The above analysis shows that by taking Laplace Transform from the differential equations, they become algebraic equation. After re-arrangement using partial fraction method and referring to the Table 1.1 the solution can be obtained. Fortunately, there is no need to solve complicated Laplace Transforms. There are certain pa- rameters that the performance of a system for various input signal can be obtained.
The closed loop control of velocity and angular position and the effect of external torque will be discussed in different chapters.