PRODUCING ROTATION
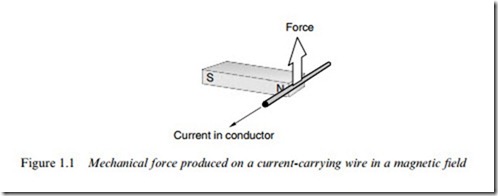
Nearly all motors exploit the force which is exerted on a current- carrying conductor placed in a magnetic Weld. The force can be demonstrated by placing a bar magnet near a wire carrying current (Figure 1.1), but anyone trying the experiment will probably be dis- appointed to discover how feeble the force is, and will doubtless be left wondering how such an unpromising eVect can be used to make eVective motors.
We will see that in order to make the most of the mechanism, we need to arrange a very strong magnetic Weld, and make it interact with many conductors, each carrying as much current as possible. We will also see later that although the magnetic Weld (or ‘excitation’) is essential to the working of the motor, it acts only as a catalyst, and all of the mechanical output power comes from the electrical supply to the conductors on which the force is developed. It will emerge later that in some motors the parts of the machine responsible for the excitation and for the energy converting functions are distinct and self-evident. In the d.c. motor, for example, the excitation is provided either by permanent magnets or by Weld coils wrapped around clearly deWned projecting Weld poles on the stationary part, while the conductors on which force is developed are on the rotor and supplied with current via sliding brushes. In many motors, however, there is no such clear-cut physical distinction between the ‘excitation’ and the ‘energy-converting’ parts of the machine, and a single stationary winding serves both purposes. Nevertheless, we will Wnd that identifying and separating the excitation and energy-converting functions is always helpful in understanding how motors of all types operate.
Returning to the matter of force on a single conductor, we will Wrst look at what determines the magnitude and direction of the force,
before turning to ways in which the mechanism is exploited to produce rotation. The concept of the magnetic circuit will have to be explored, since this is central to understanding why motors have the shapes they do. A brief introduction to magnetic Weld, magnetic Xux, and Xux density is included before that for those who are not familiar with the ideas involved.
Magnetic field and magnetic flux
When a current-carrying conductor is placed in a magnetic Weld, it experi- ences a force. Experiment shows that the magnitude of the force depends directly on the current in the wire, and the strength of the magnetic Weld, and that the force is greatest when the magnetic Weld is perpendicular to the conductor.
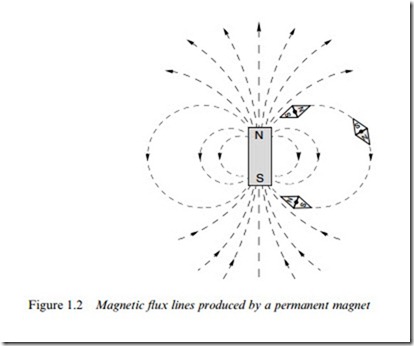
In the set-up shown in Figure 1.1, the source of the magnetic Weld is a bar magnet, which produces a magnetic Weld as shown in Figure 1.2.
The notion of a ‘magnetic Weld’ surrounding a magnet is an abstract idea that helps us to come to grips with the mysterious phenomenon of
magnetism: it not only provides us with a convenient pictorial way of picturing the directional eVects, but it also allows us to quantify the ‘strength’ of the magnetism and hence permits us to predict the various eVects produced by it.
The dotted lines in Figure 1.2 are referred to as magnetic Xux lines, or simply Xux lines. They indicate the direction along which iron Wlings (or small steel pins) would align themselves when placed in the Weld of the bar magnet. Steel pins have no initial magnetic Weld of their own, so there is no reason why one end or the other of the pins should point to a particular pole of the bar magnet.
However, when we put a compass needle (which is itself a permanent magnet) in the Weld we Wnd that it aligns itself as shown in Figure 1.2. In the upper half of the Wgure, the S end of the diamond-shaped compass settles closest to the N pole of the magnet, while in the lower half of the Wgure, the N end of the compass seeks the S of the magnet. This immediately suggests that there is a direction associated with the lines of Xux, as shown by the arrows on the Xux lines, which conventionally are taken as positively directed from the N to the S pole of the bar magnet.
The sketch in Figure 1.2 might suggest that there is a ‘source’ near the top of the bar magnet, from which Xux lines emanate before making their way to a corresponding ‘sink’ at the bottom. However, if we were to look at the Xux lines inside the magnet, we would Wnd that they were continuous, with no ‘start’ or ‘Wnish’. (In Figure 1.2 the internal Xux lines have been omitted for the sake of clarity, but a very similar Weld pattern is produced by a circular coil of wire carrying a d.c. See Figure 1.6 where the continuity of the Xux lines is clear.). Magnetic Xux lines always form closed paths, as we will see when we look at the ‘magnetic circuit’, and draw a parallel with the electric circuit, in which the current is also a continuous quantity. (There must be a ‘cause’ of the magnetic Xux, of course, and in a permanent magnet this is usually pictured in terms of atomic-level circulating currents within the magnet material. Fortunately, discussion at this physical level is not necessary for our purpose.)
Magnetic flux density
Along with showing direction, the Xux plots also convey information about the intensity of the magnetic Weld. To achieve this, we introduce the idea that between every pair of Xux lines (and for a given depth into the paper) there is a same ‘quantity’ of magnetic Xux. Some people have no diYculty with such a concept, while others Wnd that the notion of quantifying something so abstract represents a serious intellectual challenge. But whether the approach seems obvious or not, there is no denying of the practical utility of quantifying the mysterious stuV we call magnetic Xux, and it leads us next to the very important idea of magnetic Xux density (B).
When the Xux lines are close together, the ‘tube’ of Xux is squashed
into a smaller space, whereas when the lines are further apart the same tube of Xux has more breathing space. The Xux density (B) is simply the Xux in the ‘tube’ (F) divided by the cross sectional area (A) of the tube, i.e.
The Xux density is a vector quantity, and is therefore often written in bold type: its magnitude is given by equation (1.1), and its direction is that of the prevailing Xux lines at each point. Near the top of the magnet in Figure 1.2, for example, the Xux density will be large (because the Xux is squashed into a small area), and pointing upwards, whereas on the equator and far out from the body of the magnet the Xux density will be small and directed downwards.
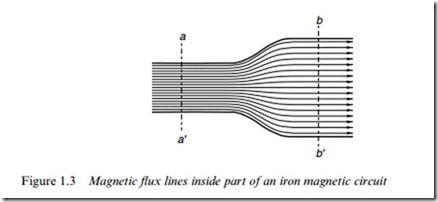
It will be seen later that in order to create high Xux densities in motors, the Xux spends most of its life inside well-deWned ‘magnetic circuits’ made of iron or steel, within which the Xux lines spread out uniformly to take full advantage of the available area. In the case shown in Figure 1.3, for example, the cross-sectional area at bb’ is twice that at aa’, but the Xux is constant so the Xux density at bb’ is half that at aa’.
It remains to specify units for quantity of Xux, and Xux density. In
the SI system, the unit of magnetic Xux is the weber (Wb). If one weber of Xux is distributed uniformly across an area of 1m2 perpendicular to the Xux, the Xux density is clearly one weber per square metre
(Wb=m2). This was the unit of magnetic flux density until about 40 years ago, when it was decided that one weber per square meter would henceforth be known as one tesla (T), in honour of Nikola Tesla who is generally credited with inventing the induction motor. The widespread use of B (measured in tesla) in the design stage of all types of electro- magnetic apparatus means that we are constantly reminded of the importance of tesla; but at the same time one has to acknowledge that the outdated unit did have the advantage of conveying directly what Xux density is, i.e. Xux divided by area.
In the motor world we are unlikely to encounter more than a few milliwebers of Xux, and a small bar magnet would probably only pro- duce a few microwebers. On the other hand, values of Xux density are typically around 1 T in most motors, which is a reXection of the fact that although the quantity of Xux is small, it is also spread over a small area.
Force on a conductor
We now return to the production of force on a current-carrying wire placed in a magnetic Weld, as revealed by the setup shown in Figure 1.1.
The direction of the force is shown in Figure 1.1: it is at right angles to both the current and the magnetic Xux density. With the Xux density horizontal and to the right, and the current Xowing out of the paper, the force is vertically upward. If either the Weld or the current is reversed, the force acts downwards, and if both are reversed, the force will remain upward.
We Wnd by experiment that if we double either the current or the Xux density, we double the force, while doubling both causes the force to increase by a factor of four. But how about quantifying the force? We need to express the force in terms of the product of the current and the magnetic Xux density, and this turns out to be very straightforward when we work in SI units.
The force on a wire of length l, carrying a current I and exposed to a uniform magnetic Xux density B throughout its length is given by the simple expression
where F is in newtons when B is in tesla, I in amperes, and l in metres. This is a delightfully simple formula, and it may come as a surprise to some readers that there are no constants of proportionality involved in equation 1.2. The simplicity is not a coincidence, but stes from the fact that the unit of current (the ampere) is actually deWned in terms of force.
Strictly, equation 1.2 only applies when the current is perpendicular to the Weld. If this condition is not met, the force on the conductor will be less; and in the extreme case where the current was in the same direction as the Weld, the force would fall to zero. However, every sensible motor designer knows that to get the best out of the magnetic Weld it has to be perpendicular to the conductors, and so it is safe to assume in the subsequent discussion that B and I are always perpendicular. In the remainder of this book, it will be assumed that the Xux density and current are mutually perpendicular, and this is why, although B is a vector quantity (and would usually be denoted by bold type), we can drop the bold notation because the direction is implicit and we are only interested in the magnitude.
The reason for the very low force detected in the experiment with the bar magnet is revealed by equation 1.2. To obtain a high force, we must have a high Xux density, and a lot of current. The Xux density at the ends of a bar magnet is low, perhaps 0.1 tesla, so a wire carrying 1 amp will experience a force of only 0.1 N/m (approximately 100 gm wt). Since the Xux density will be conWned to perhaps 1 cm across the end face of the magnet, the total force on the wire will be only 1 gm. This would be barely detectable, and is too low to be of any use in a decent motor. So how is more force obtained?
The Wrst step is to obtain the highest possible Xux density. This is achieved by designing a ‘good’ magnetic circuit, and is discussed next. Secondly, as many conductors as possible must be packed in the space where the magnetic Weld exists, and each conductor must carry as much current as it can without heating up to a dangerous temperature. In this way, impressive forces can be obtained from modestly sized devices, as anyone who has tried to stop an electric drill by grasping the chuck will testify.