EFFICIENCY AND POWER FACTOR

The efficiency η has already been defined, both for motoring and generating, earlier in this chapter. The power factor cosϕ₁ may be defined in relation to the equivalent circuit as

cosϕ =₁ Z_e (7.76)

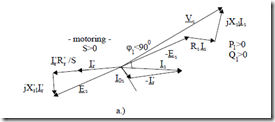
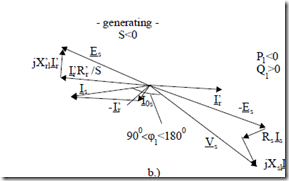
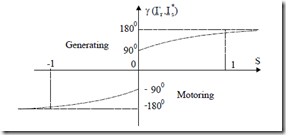
Figure 7.9 shows that Re is negative for the actual generating mode. This explains why in (7.76) the absolute value of R_e is used. The power factor, related to reactive power flow, has the same formula for both motoring and generating, while the efficiency needs separate formulas (7.50) and (7.53). The dependence of efficiency and power factor on load (slip or speed) is essential when the machine is used for variable load (Figure 7.20).

 

Figure 7.20 IM efficiency, η, power factor, cosϕ, and slip, S/S_n versus relative power load at the shaft: P_2m/P_n

Such curves may be calculated strictly based on the equivalent circuit (Figure 7.1) with known (constant or variable) parameters, and given values of slip. Once the currents are known all losses and input power may be calculated. The mechanical losses may be lumped into the core loss resistance R_1m or, if not, they have to be given from calculations or tests performed in advance. For applications with highly portable loads rated from 0.25 – to 1.5 the design of the motor has to preserve a high efficiency.

A good power factor will reduce VAR compensation hardware ratings and costs, as an industrial plant average power factor should not be lagging below 0.95 to avoid VAR penalties.

Example 7.5. Motor performance

An induction motor with deep bars is characterized by rated power P_n = 20 kW, supply line voltage V_sl = 380 V (star connection), f₁ = 50 Hz, η_n = 0.92, p_mec =

0.005 P_n, p_iron = 0.015 P_n, p_s = 0.005 P_n, p_cosn = 0.03 P_n, cosϕ_n = 0.9, p₁ = 2, starting current I_sc = 5.2I_n, power factor cosϕ_sc = 0.4, and no-load current I_on =

0.3I_n.

Let us calculate

a.) Rotor cage losses p_corn, electromagnetic power P_elm, slip, S_n, speed, n_n, rated current I_n and rotor resistance R_r′, for rated load

b.) Stator resistance R_s and rotor resistance at start R_rs′

c.) Electromagnetic torque for rated power and at start

d.) Breakdown torque

Solution

a.) Based on (7.50), we notice that, at rated load, we lack the rotor cage losses, p_corn from all losses.

pcorn = _ηPⁿ_n ⁻ (pcosn + pSn + piron + piron )− Pn = (7.77)

W

On the other hand, the rated current In comes directly from the power input expression

I_n A (7.78)

The slip expression (7.52) yields
Sn = Pn −pcosnpcorn−pSn −piron ηn = 639.13	= =	(7.79)

0.0308

−(0.03+0.005+0.015 20000)

The rated speed nn is
nn = Pf11 (1−Sn )= 502 (1− 0.0308)= 24.23rps =1453.8rpm The electromagnetic power Pelm is	(7.80)
Pelm = pcorn = 639.13 = 20739W	(7.81)

Sn 0.0308

To easily find the rotor resistance, we need the rotor current. At rated slip, the rotor circuit is dominated by the resistance R_r′/S_n and thus the no-load (or magnetizing current) I_0n is about 90⁰ behind the rotor resistive current I_rn′. Thus, the rated current I_n is

I_rn‘== 35.05A (7.83)

Now the rotor resistance at load Rr′ is
R ‘r = pcornrn 2 = 3639⋅35..05132 = 0.1734Ω 3I ‘ b.) The stator resistance Rs comes from	(7.84)

R_s (7.85)

The starting rotor resistance Rrs′ is obtained based on starting data:
R ‘= Vsl cosϕsc − R = 380 0.4 − 0.148 = 0.31186Ω	(7.86)

rs 3 Isc s 3 5.2⋅36.742

Notice that K_r (7.87)

This is mainly due to skin effect.

c.) The rated electromagnetic torque T_en is

T_en Nm (7.88)

The starting torque T_es is

Tes Nm (7.89)

T /T_{es en} =108.76/132.095 = 0.833

d.) For the breakdown torque, even with approximate formula (7.71), the short-circuit reactance is needed. From starting data,

Xsc = Vsl3 sinIscϕsc = 3803 5.21⋅−360.4.6722 =1.0537Ω (7.90)

The rotor leakage reactance X_rls = X_sc – X_sl = 1.0537 – 0.65 = 0.4037 Ω. Due to skin effect and leakage saturation, this reactance is smaller than the one “acting” at rated load and even at breakdown torque conditions. Knowing that K_r = 1.758 (7.87), resistance correction coefficient value due to skin effect, we could find K_x ≈ 0.9 from Chapter 8, for a rectangular slot.

With leakage saturation effects neglected the rotor leakage reactance at critical slip S_k (or lower) is

X ‘_rl K_x X ‘ (7.91)

Now, with C1 ≈ 1 and Rs ≈ 0, from (7.71) the breakdown torque T_ek is

Tek ≈ 3 Vsl 2 p 

 3  ω11 2(Xsl1+ X ‘rl ) = (7.92)

Nm

The ratio T_ek/T_en is

Tek /Ten = 422.68 = 3.20

132.095

This is an unusually large value facilitated by a low starting current and a high power factor at start; that is, a low leakage reactance X_sc was considered.

PHASOR DIAGRAMS: STANDARD AND NEW

The IM equations under steady state are, again,

I_s (R_s + jX_sl )−V_s = E_s



_Ir ‘_ R ‘r + jX ‘

E_s= −_S Z_1m(I_srl+_I+_r ‘)V_S= −r ‘ ₌Z₁E_{m 0s}sI

=

Z1m RR11mm+⋅ jXjX11mm = R1ms + jX1ms

R1m >> X1m; R1ms << X1ms; R1ms << R1m; X1ms ≈ X1m (7.93)

They can be and have been illustrated in phasor diagrams. Such diagrams for motoring (S > 0) and generating (S < 0) are shown in Figure 7.21a and b, for

V_r′ = 0 (short-circuited rotor).

As expected, for the short-circuited rotor, the reactive power remains positive for generating (Q₁ > 0) as only the active stator current changes sign from motoring to generating.

PQ1 ==3V3Vs IssIcossinϕ <>ϕ >11 00 (7.94)

1

Today the phasor diagrams are used mainly to explain IM action, while, before the occurrence of computers, they served as a graphical method to determine steady-state performance without solving the equivalent circuit.

However, rather recently the advance of high performance variable speed a.c. drives has led to new phasor (or vector) diagrams in orthogonal axis models of an ac machine. Such vector diagrams may be accompanied by similar phasor diagrams valid for each phase of a.c. machines. To simplify the derivation let us neglect the core loss (R_1m ≈ ∞ or R_1ms = 0). We start by defining three flux linkages per phase: stator flux linkage Ψ_s, rotor flux linkage Ψ_r‘, and airgap (magnetizing) Ψ_m.

ψs = LslIs + ψm

ψ_r ‘= L ‘_rl I_r ‘+ψ_m (7.95) ψm = L1m(Is + Ir ‘)= L1m Im

E_s = − ωj ₁L_1m I_m = − ωj ₁ψ_m (7.96)

 

 

Figure 7.21 Standard phasor diagrams, a.) for motoring, b.) for generating

The stator and rotor equations in (7.93) become
IsRs − Vs = − ωj 1ψs	(7.97)
Ir’ R ‘r + Vr ‘ = − ωj 1ψr ‘	(7.98)

S S

For zero rotor voltage (short-circuited rotor), Equation (7.98) becomes:

I_r ‘ ^{R ‘}S^r = − ωj ₁ψ_r ‘; V_r ‘= 0 (7.99)

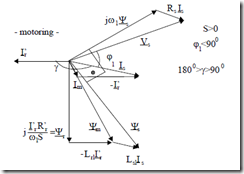
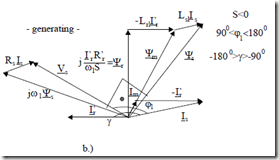
Equation (7.99) shows that at steady state, for V_r′ = 0, the rotor current I_r′ and rotor flux Ψ_r′ are phase shifted by 90⁰.

Consequently, the torque T_e expression (7.60) becomes:

Te = 3R ‘I ‘rS r 2 ωp11 = 3p1ψr ‘I ‘r (7.100)

Equation (7.100) may be considered the basis for modern (vector) IM control. For constant rotor flux per phase amplitude (RMS), the torque is proportional to rotor phase current amplitude (RMS). With these new variables, the phasor diagrams based on Equations (7.97) and (7.98) are shown in Figure 7.22.

Such phasor diagrams could be instrumental in computing IM performance when fed from a static power converter (variable voltage, variable frequency).

Figure 7.22 Phasor diagram with stator, rotor and magnetization flux linkages, Ψ_r′,  Ψ_m, Ψ_s 

a.) motoring b.) generating (continued

Figure 7.22 (continued)

The torque expression may also be obtained from (7.97) by taking the real part of it after multiplication by I_s^*.

Re 3[ I_{s s}I ^*R_s + 3jω₁ψ_sI_s^*]= 3Re(V I_{s s}^*) (7.101)

The second term in (7.101), with core loss neglected, is, in fact, the electromagnetic power P_elm

	Pelm = ω3 1 Imag(ψs Is*)= Te(ω1 /p1)	(7.102)
	Te = 3p Imag1 (ψs Is*)= 3p L1 1m Imag(Ir ‘Is*)	(7.103)
or	Te = 3p L1 1m Ir ‘Is sin ; γ γ > 900	(7.104)

In (7.104), γ is the angle between the rotor and stator phase current phasors with γ > 0 for motoring and γ < 0 for generating.

 

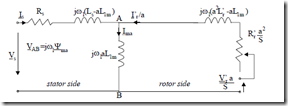
Now, from the standard equivalent circuit (Figure 7.1 with R_1m ≈ ∞),

Ir’= −Is R ‘Sr + ωjjω11(LL11mm + L ‘rl ) (7.105)

So the angle γ between I_r′ and I_s^* depends on slip S and frequency ω₁ and motor parameters (Figure 7.23). It should be noted that the angle γ is close to ±180⁰ for S = ±1 and close to ±90⁰ toward |S| = 0. 

ALTERNATIVE EQUIVALENT CIRCUITS

Alternative equivalent circuits for IMs abound in the literature. Here we will deal with some that have become widely used in IM drives. In essence [2], a new rotor current is introduced.

I_ra ‘^{= I}a^r‘ (7.106)

Using this new variable in (7.95) through (7.98), we easily obtain:

IsRs + ωj 1[Ls −aL1m ]Is −Vs = Ea

Ea = − ω ψj 1 ma; ψma = aL1m(Is + Ira ‘ ; ) Ima = Is + Iar ‘ (7.107)

Ira ‘R ‘ar 2 + ωj 1(aL ‘ Lr − 1m )aIra ‘+ V ‘aSr = Ea

Figure 7.24 General equivalent circuit (core loss neglected)

For a = 1, we reobtain, as expected, Equations (7.95) through (7.98). L_s, L_r′ represent the total stator and rotor inductances per phase when the IM is threephase fed.

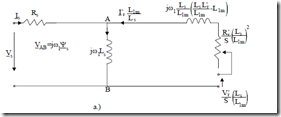
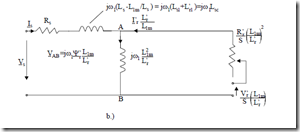
Now the general equivalent circuit of (7.107), similar to that of Figure 7.1, is shown in Figure 7.24. For a = 1, the standard equivalent circuit (Figure 7.1) is obtained. If a = L_s/L_1m ≈ 1.02 – 1.08, the whole inductance (reactance) is occurring in the rotor side of equivalent circuit and Ψ_ma = Ψ_s (Figure 7.25a). The equivalent circuit directly evidentiates the stator flux.

 

Figure 7.25 Equivalent circuit

a.) with stator flux shown b.) with rotor flux shown

For a = L_1m/L_r′ ≈ 0.93 – 0.97, ψ_ma ^{= L} _{L ‘}^1m_r ψ_r ‘, the equivalent circuit is said

to evidentiate the rotor flux.

Advanced IM control is performed at constant stator, Ψ_s, rotor Ψ_r, or magnetization flux, Ψ_m amplitudes. That is voltage and frequency, V_s, f₁, are changed to satisfy such conditions.

Consequently circuits in Figure 7.25 should be instrumental in calculating IM steady-state performance under such flux linkage constraints.

Alternative equivalent circuits to include leakage and main saturation and skin effect are to be treated in Chapter 8.

Example 7.6. Flux linkage calculations

A cage-rotor induction motor has the following parameters: R_s = 0.148Ω, X_sl = X_rl′ = 0.5Ω, X_m = 20Ω, 2p₁ = 4poles, V_s = 220V/phase (RMS)–star connection, f₁ = 50Hz, rated current I_sn = 36A, cosϕ_n = 0.9. At start, the current

I_start = 5.8I_n, cosϕ_start = 0.3.

Let us calculate the stator, rotor and magnetization flux linkages Ψ_s, Ψ_r′. Ψ_m at rated speed and at standstill (core loss is neglected). With S = 0.02, calculate the rotor resistance at full load.

Solution

To calculate the RMS values of Ψ_s, Ψ_r′. Ψ_m we have to determine, in fact, V_AB on Figure 7.24, for a_s = L_s/L_1m, a_r = L_1m/L_r′ and a_m = 1, respectively.

ψs 2 = 2 Vsω−1 IsRr (7.108)

ψr ‘ 2 = 2

V − I Rr − I jω1 Lsl + L ‘rl

s s  sL1m ( ) (7.109)

ω1 L ‘r  

V

ω1
Is = I coss( ϕ − jsin ϕ)	(7.111)

ψm 2 = 2 s − IsRr − Is jω1Lsl (7.110)

These operations have to be done twice, once for I_s = I_n, cosϕ_n and once for

Is = Istart, cosϕstart.

For I_n = 36A, cosϕ_n = 0.9,

ψ_s 2 = 2 220−36⋅(20.9_π50− j4359)0.148 = 0.9654Wb

ψ ‘ 2 = 2 220−36⋅(0.9− j4359)(0.148+ j1⁾ ₌ 0.9314Wb (7.112) r 2π50_ 20 _

 20.5

ψ_m 2 = 2 220 −36⋅(0.92_π−50j4359)(0.148+ j1) = 0.9369Wb (7.113)

The same formulas are applied at zero speed (S = 1), with starting current and power factor,

(ψs 2)start = 2 220−36⋅5.8 0.32⋅(π50− j0.888)⋅0.148 = 0.9523Wb

(ψ_r ‘ 2)_start = 2 220−36⋅5.8 0.32π⋅50( _ −20j0.888_ )(0.148+ j1) = 0.1998Wb(7.114)

 20.5

(ψm 2)start = 2 220−36⋅5.8 0.3⋅(2π50− j0.888)(0.148+ j1) = 0.5306Wb

The above results show that while at full load the stator, magnetization and rotor flux linkage amplitudes do not differ much, they do so at standstill. In particular, the magnetization flux linkage is reduced at start to 55−65% of its value at full load, so the main magnetic circuit of IMs is not saturated at standstill.