Hexadecimal numbers
The hexadecimal number system is used primarily for entering and reading data of microprocessor-based 4-, 8-, 16-, 32-, and 64-bit systems. Using hexadecimal numbers allows the breaking of a binary number into groups of four to reduce chance of error when entering data.
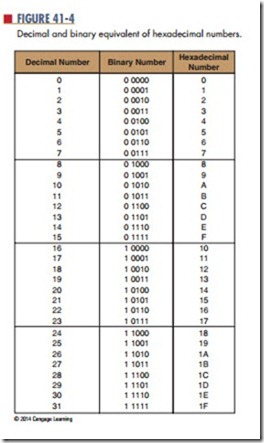
The hexadecimal number system is referred to as base 16. There are 16 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. Figure 41-4 shows
hexadecimal numbers with their decimal and binary equivalents. The advantage of hexadecimal numbers is that they are converted directly from 4 bits of binary numbers.
To convert binar y to a hexadecimal number requires dividing the binary number into groups of four, starting from the right, as shown by the following example:
To convert a hexadecimal number to a binary equivalent requires reversing the process and converting the hexadecimal number to binary groups of four, as shown by the following example:
EXAMPLE:
Hexadecimal number: 6A7F4D2C16
Separate the numbers: 6 A 7 F 4 D 2 C16
Convert to binary:
0011 1010 0111 1111 0100 1101 0010 11002
Binary equivalent:
001110100111111101001101001011002
Lead zeros can be dropped, resulting in:
1110100111111101001101001011002
Like binary numbers, each hexadecimal number is a weighted number with a place value. The value of a hexadecimal number can be determined by adding the product of each digit and its place value. Figure 41-5 shows hexadecimal place values. The method for converting a hexadecimal number to a decimal is shown by the following example: