Binary number System:Binary numbers

Anumber system is nothing more than a code. For each distinct quantity, there is an assigned symbol. When the code is learned, counting can be accomplished. This leads to arithmetic and higher forms of mathematics.

The simplest number system is the binary number system. The binary system contains only two digits, 0 and 1. These digits have the same value as in the decimal number system.

The binary number system is used in digital and microprocessor circuits because of its simplicity. Bi- nary data are represented by binary digits, called bits. The term bit is derived from binary digit.

Binary numbers

The decimal system is called a base-10 system be- cause it contains 10 digits, 0 through 9. The binary number system is a base-2 system because it contains two digits, 0 and 1. The position of the 0 or 1 in a binary number indicates its value within the number. This is referred to as its place value or weight. The place value of the digits in a binary number increases by powers of two.

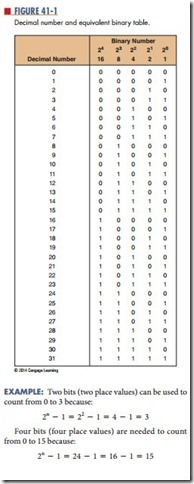
Counting in binary starts with the numbers 0 and 1. When each digit has been used in the 1’s place, another digit is added in the 2’s place and the count continues with 10 and 11. This uses up all combinations of two digits, so a third digit is added in the 4’s place and the count continues with 100, 101, 110, and 111. Now a fourth digit is needed in the 8’s place to continue, and so on. Figure 41-1 shows the binary counting sequence.

To determine the largest value that can be repre- sented by a given number of places in base 2, use the following formula:

where n represents the number of bits (or number of place values used).