The Sine Wave
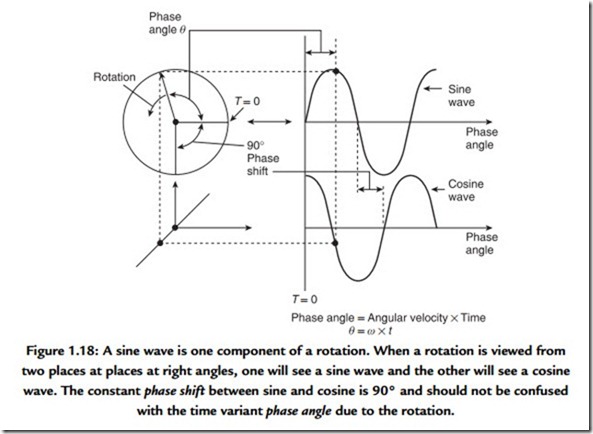
As the sine wave is such a useful concept it will be treated here in detail. Figure 1.18 shows a constant speed rotation viewed along the axis so that the motion is circular. Imagine, however, the view from one side in the plane of the rotation. From a distance, only a vertical oscillation will be observed and if the position is plotted against time the resultant waveform will be a sine wave. Geometrically, it is possible to calculate the height or displacement because it is the radius multiplied by the sine of the phase angle.
The phase angle is obtained by multiplying the angular velocity ω by the time t. Note that the angular velocity is measured in radians per second, whereas frequency f is measured in rotations per second or hertz. As a radian is unit distance at unit radius (about 57°), then there are 2π radians in one rotation. Thus the phase angle at a time t is given by sinωt or sin2πft.
A second viewer, who is at right angles to the first viewer, will observe the same waveform but with different timing. The displacement will be given by the radius multiplied by the cosine of the phase angle. When plotted on the same graph, the two waveforms are phase shifted with respect to one another. In this case the phase shift is 90° and the two waveforms are said to be in quadrature. Incidentally, the motions on each side of a steam locomotive are in quadrature so that it can always get started (the term used is quartering). Note that the phase angle of a signal is constantly changing with time, whereas the phase shift between two signals can be constant. It is important that these two are not confused.
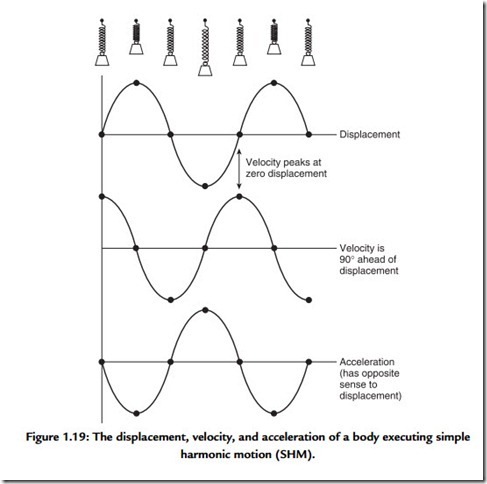
The velocity of a moving component is often more important in audio than the displacement. The vertical component of velocity is obtained by differentiating the displacement. As the displacement is a sine wave, the velocity will be a cosine wave whose amplitude is proportional to frequency. In other words, the displacement and velocity are in quadrature with the velocity lagging. This is consistent with the velocity reaching a minimum as the displacement reaches a maximum and vice versa. Figure 1.19 shows displacement, velocity, and acceleration waveforms of a body executing simple harmonic motion (SHM). Note that the acceleration and the displacement are always antiphase.