Frequency Discrimination
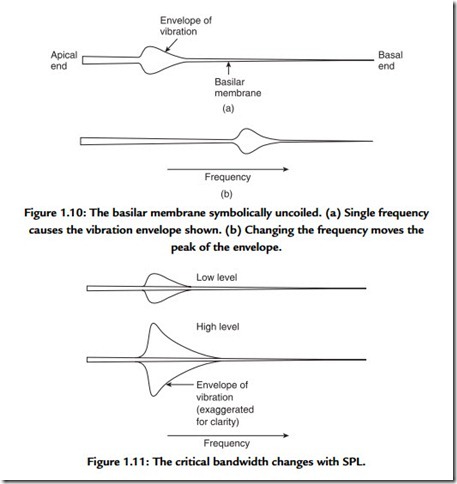
Figure 1.10 shows an uncoiled basilar membrane with the apex on the left so that the usual logarithmic frequency scale can be applied. The envelope of displacement of the basilar membrane is shown for a single frequency at Figure 1.10(a). The vibration of the membrane in sympathy with a single frequency cannot be localized to an infinitely small area, and nearby areas are forced to vibrate at the same frequency with an amplitude that decreases with distance. Note that the envelope is asymmetrical because the membrane is tapering and because of frequency-dependent losses in the propagation of vibrational energy down the cochlea. If the frequency is changed, as in Figure 1.10(b), the position of maximum displacement will also change. As the basilar membrane is continuous, the position of maximum displacement is infinitely variable, allowing extremely good pitch discrimination of about one-twelfth of a semitone, which is determined by the spacing of hair cells.
In the presence of a complex spectrum, the finite width of the vibration envelope means that the ear fails to register energy in some bands when there is more energy in a nearby band. Within those areas, other frequencies are mechanically excluded because their amplitude is insufficient to dominate the local vibration of the membrane. Thus the Q factor of the membrane is responsible for the degree of auditory masking, defined as the decreased audibility of one sound in the presence of another. Masking is important because audio compression relies heavily on it.
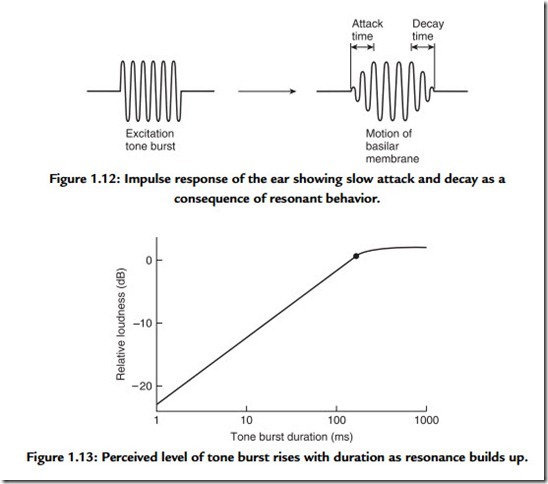
The term used in psychoacoustics to describe the finite width of the vibration envelope is critical bandwidth. Critical bands were first described by Fletcher.5 The envelope of basilar vibration is a complicated function. It is clear from the mechanism that the area of the membrane involved will increase as the sound level rises. Figure 1.11 shows the bandwidth as a function of level.
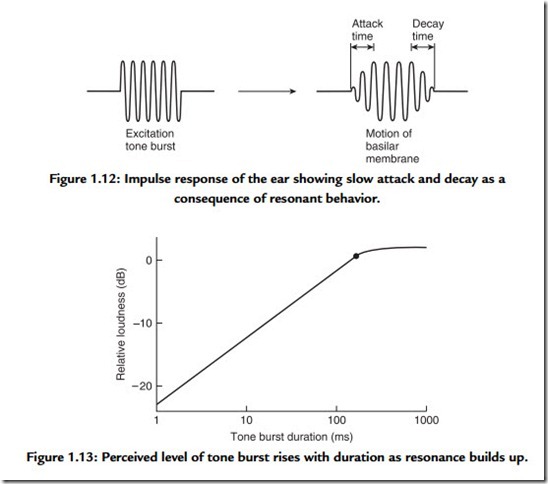
As seen elsewhere, transform theory teaches that the higher the frequency resolution of a transform, the worse the time accuracy. As the basilar membrane has finite frequency resolution measured in the width of a critical band, it follows that it must have finite time resolution. This also follows from the fact that the membrane is resonant, taking time to start and stop vibrating in response to a stimulus. There are many examples of this. Figure 1.12 shows the impulse response. Figure 1.13 shows that the perceived loudness of a tone burst increases with duration up to about 200 ms due to the finite response time.
The ear has evolved to offer intelligibility in reverberant environments, which it does by averaging all received energy over a period of about 30 ms. Reflected sound that arrives within this time is integrated to produce a louder sensation, whereas reflected sound that arrives after that time can be temporally discriminated and perceived as an echo.
Microphones have no such ability, which is why acoustic treatment is often needed in areas where microphones are used.
A further example of the finite time discrimination of the ear is the fact that short interruptions to a continuous tone are difficult to detect. Finite time resolution means that masking can take place even when the masking tone begins after and ceases before the masked sound. This is referred to as forward and backward masking.
Figure 1.14(a) shows an electrical signal in which two equal sine waves of nearly the same frequency have been added together linearly. Note that the envelope of the signal varies as the two waves move in and out of phase. Clearly the frequency transform calculated to infinite accuracy is that shown at Figure 1.14(b). The two amplitudes are constant and there is no evidence of envelope modulation. However, such a measurement requires an infinite time. When a shorter time is available, the frequency discrimination of the transform falls and the bands in which energy is detected become broader.
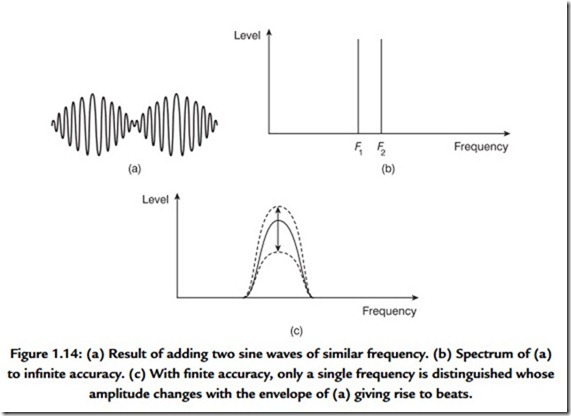When the frequency discrimination is too wide to distinguish the two tones as shown in Figure 1.14(c), the result is that they are registered as a single tone. The amplitude of the single tone will change from one measurement to the next because the envelope is being measured. The rate at which the envelope amplitude changes is called beat frequency, which is not actually present in the input signal. Beats are an artifact of finite frequency resolution transforms. The fact that human hearing produces beats from pairs of tones proves that it has finite resolution.