Velocity of Sound
For a given frequency, the relation of the wavelength to the velocity of sound in the medium is
where λ is the wavelength in feet or meters, c is the velocity of sound in ft/s or m/s, and f is the frequency in Hz.
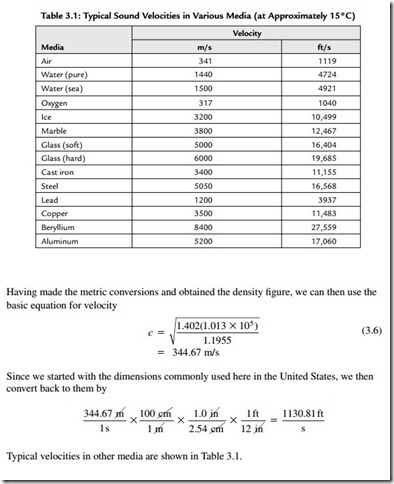
In dealing with many acoustic interactions, the wavelength involved is significant and the ability to calculate it is important. Therefore we need to be able to both calculate and measure the velocity of sound quickly and accurately.
The velocity of sound varies with temperature to a degree sufficient to require our alertness to it. A knowledge of the exact velocity of sound when using signal-delayed signal analysis allows very precise distance measurements to be made by observing the frequency interval between comb filters from two sources and then converting from frequency to time and finally to distance.
The velocity of sound under conditions likely to be encountered in connection with architectural acoustic considerations is dependent on three fundamental factors. These are:
1. γ is the ratio of specific heats and is 1.402 for diatomic molecules (air molecules).
2. PS is the equilibrium gas pressure in Newtons per square meter (1.013 X 105 N/m2).
3. ρ is the density of air in kilograms per cubic meter (kg/m3)
where c is the velocity of sound in m/s.
The density of air varies with temperature, and an examination of the basic equations reveals that, indeed, temperature variations are the predominant influence on the velocity of sound in air.
The equation for calculating the density of air is
where density of air is in kg/m3; H is the barometric pressure in centimeters of mercury, Hg; °C is the temperature in degrees Celsius; 9/5 (°C) + 32 = °F; and 5/9 (°F) –32 = °C. Hg in inches times 2.54 equals Hg in centimeters.
3.4.1 Example
If we were to measure a temperature of 72°F and a barometric pressure of 29.92 in cm Hg, we would first calculate the density of the air according to data gathered: