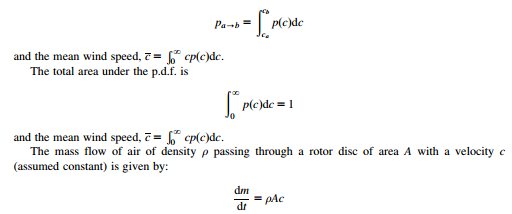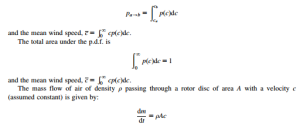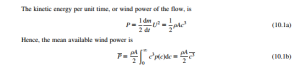Annual energy output
The cost effectiveness of a wind turbine is determined by its average production of energy over a year. (Of course, some allowance must be made for installation and running costs.) Determining the annual energy output requires detailed information about the wind speed frequency distribution, derived from detailed measurements of the wind speed variation at the actual site of the wind turbine. For a HAWT, it is necessary to measure the varying wind speed at the elevation of the turbine’s hub over a long period of time, usually over at least a year. The usual procedure adopted is to make these varying wind speed measurements over relatively short time intervals, say 5 min and the averaged values are stored in what are called “wind speed bins.” This “method of bins” is widely adopted as a reliable way of summarizing wind data.3
Statistical analysis of wind data Basic equations
The frequency of the occurrence of wind speeds can be described by a p.d.f. p(c), of the wind speed c. The probability of a particular value of a wind speed occurring between ca and cb may be expressed as
Wind speed probability distributions
For the statistical analysis of wind speed distributions, two types of flow model are in use. These are
1. the Rayleigh Distribution;
2. the Weibull Distribution.
The simplest velocity probability distribution for the wind resource is the so-called Rayleigh distribution as it only requires knowledge of one parameter namely the mean wind speed c.
The Rayleigh probability distribution is written as
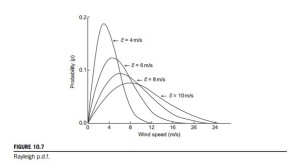
Figure 10.7 illustrates Rayleigh probability density distributions for a range of different mean wind speeds. It is implied that a bigger value of the mean wind speed gives a higher probability of higher wind speeds. The cumulative distribution function FðcÞ represents the time fraction that the wind speed is smaller than or equal to a given wind speed, c. This means that FðcÞ 5 the probability that c0 # c where c0 is a dummy variable:
It can be shown that
Note: The mathematics of the Weibull probability distribution are rather more complicated than those of the Rayleigh distribution as it is based upon two parameters and also requires some knowledge of Gamma functions. All we need to know about the wind speed characteristics, for the purposes of this book, can be obtained using the Rayleigh probability distribution function.
Readers wishing to advance their knowledge of the Weibull probability function and its application to wind characteristics can consult Manwell et al. (2009).
Comment: It should be carefully noted that the mean power output of a wind turbine (which includes the effect of the probability function), Eq. (10.1b), is very much less than the rated power of the turbine. This has been a source of some confusion in discussions. The ratio of the mean power produced at a given mean wind speed to the so-called rated power output is called the capacity factor. The capacity factor is usually about 0.5 at maximum power output of a turbine.