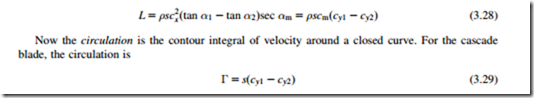Analysis of cascade forces
Lift and drag coefficients are frequently referred to in the general literature and in many later parts of this book, especially with regard to low-speed fans and wind turbines. However, with the advent of much higher blade speeds in compressors and turbines, the effects of compressibility have become complicated matters and their usage has almost vanished. Instead, it is now common practice just to use flow deflection and nondimensional total pressure loss in calculating performance, as described previously. This section is included for completeness, but it should be remembered that the material is, strictly speaking, only applicable to low- speed turbomachines.
Consider a portion of a compressor blade cascade, as shown in Figure 3.10. The forces X and Y exerted by a unit depth of blade upon the fluid are exactly equal and opposite to the forces exerted by the fluid upon the blade. A control surface is drawn with end boundaries far upstream and downstream of the cascade and with side boundaries coinciding with the median streamlines.
Circulation and lift
Note: The classical analysis of the lift developed by a single isolated aerofoil is based upon the ideal case, when D 5 0, and the flow is incompressible, i.e., ρ is constant.
The Kutta-Joukowski theorem states that the lift force L is
where c is the relative velocity between the aerofoil and the fluid at infinity and Γ is the circulation about the aerofoil. This theorem is of fundamental importance in the development of the theory of aerofoils (Glauert, 1959).
With the assumption that stagnation pressure losses are absent, the lift force per unit span of a blade in cascade, using Eq. (3.22), becomes
As the spacing between the cascade blades is increased without limit (i.e., s-N), the inlet and outlet velocities to the cascade, c1 and c2, become equal in magnitude and direction.
Thus, c1 5 c2 5 cm and Eq. (3.30) becomes the same as the theorem of Kutta-Joukowski stated previously for an isolated aerofoil.