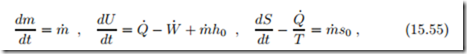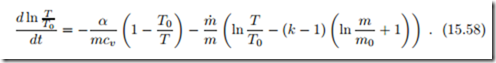Reversible Filling of a Gas Container with Heat Exchange
In the previous sections we assumed that no heat is exchanged during filling and discharge, which would be the case when the processes are rather fast. For a lower filling rate, since real containers are not adiabatic, there will be heat exchange during filling, and here we study a container with heat exchange. We assume that the container is in contact with the environment at T0, and use Newton’s law of cooling. The balances for mass, energy and entropy become
where Q˙ = α (T0 − T ) is the heat exchange between the compressed gas at T and the environment. As before, we assume that initially the container is in equilibrium with the environment, so that it contains the mass m0 = p0 V0 , and that the mass flow is constant, m˙ = const. Integration of the mass balance gives the mass in the container at time t as
After some manipulation, the second law reduces to a differential equation for the gas temperature,
Solving the first law for power, and use of the appropriate constitutive equation and the differential equation for T results in
The filling pressure follows from the ideal gas equation, p = mRT . Of course, for the adiabatic case (α = 0) the solution of Sec. 15.4 fulfills both equations.
For the non-adiabatic case, the equation for temperature cannot be solved with pencil and paper, but must be solved on a computer. The numerical solution T (t) can then be used to determine the compressor power (15.59) and the total work W = { W˙ dt. Figure 15.7 shows, in dimensionless form, mass, temperature, pressure and compressor work as functions of time, comparing the adiabatic case (α = 0, dashed), and the case with heat loss to the environment (α j= 0, continuous). Less work is required in the latter case, since, due to the constant heat loss, the temperature, and thus the pressure is lower.
For the data given with the figure, the total work requirement for filling (di-for the non-adiabatic case.
While non-adiabatic filling requires less work, the work potential of the filling (same mass) is less as well, due to lower pressure. The heat loss to the environment will continue after filling is completed. Accordingly, the filling pressure, and the work potential will drop after filling is completed. We consider the work potential (exergy) in case that the filling temperature has dropped to the environmental temperature T0. Then the state of the air in the cavern is
and then cools to environmental temperature, the work potential is only half of the filling work. Of course, irreversibilities during filling will increase the work requirement, and irreversibilities during discharge will reduce the work output below Ξ0 so that in the end the storage efficiency is relatively low.