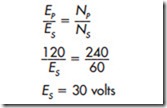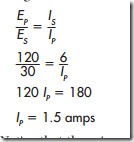TRANSFORMER CALCULATIONS
In the following examples, values of voltage, cur- rent, and turns for different transformers will be computed.
EXAMPLE
In the next example, assume that the primary winding contains 240 turns of wire and the secondary contains 1,200 turns of wire. This is a turns ratio of 1:5 (1,200/240 = 5). Now assume that 120 volts is connected to the primary winding. Compute the voltage output of the secondary winding.
The transformer in this example is known as a step-down transformer because it has a lower secondary voltage than primary voltage.
Now assume that the load connected to the secondary winding has an impedance of 5 . The next problem is to calculate the current flow in the secondary and primary windings. The current flow of the secondary can be computed using Ohm’s law since the voltage and impedance are known.
Now that the amount of current flow in the second- ary is known, the primary current can be computed using the formula:
Notice that the primary voltage is higher than the secondary voltage, but the primary current is much less than the secondary current. A good rule for transformers is that power in must equal power out. If the primary voltage and current are multiplied together, it should equal the product of the voltage and current of the secondary:
EXAMPLE
In the next example, assume that the primary winding contains 240 turns of wire and the secondary contains 1,200 turns of wire. This is a turns ratio of 1:5 (1,200/240 = 5). Now assume that 120 volts is connected to the primary winding. Compute the voltage output of the secondary winding.
Notice that the secondary voltage of this trans- former is higher than the primary voltage. This type of transformer is known as a step-up transformer.
Now assume that the load connected to the secondary has an impedance of 2,400 n. Find the amount of current flow in the primary and secondary windings. The current flow in the secondary winding can be computed using Ohm’s law.