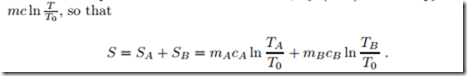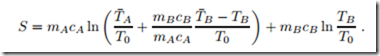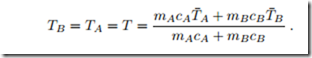Example: Equilibration of Temperature
We return to the problem considered in Sec. 3.12, the equilibration of temperature between two bodies A and B, with initial temperatures T¯A and T¯B . The first law alone was not sufficient to find the final common temperature, which will now be obtained from the second law. The compound system A+B is adiabatic to the outside, so that the second law becomes
Thus the total entropy S = SA + SB of the system will grow in time until it will assume its maximum in equilibrium, when no further changes occur.
For the simple solids under consideration, by (4.14) the entropy is S =
The first law relates the actual temperatures TA and TB of the two bodies and their initial temperatures T¯A, T¯B through (3.26). With this, the entropy of the system becomes a function of TB only,
Since the entropy of the compound system A+B can only grow, in equilibrium the entropy assumes the largest possible value, which is obtained from the conditionThe evaluation, left as an exercise for the reader, gives the expected result for the common equilibrium temperature,