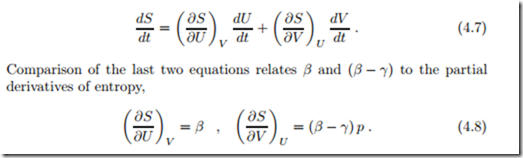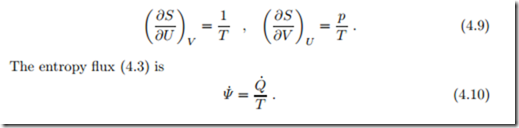Entropy Flux
In non-isolated systems, which exchange heat and work with the surroundings, we expect an exchange of entropy with the surroundings which must be added to the entropy inequality. We write
where Ψ˙ is the entropy flux. This equation states that the change of entropy in time (dS/dt) is due to transport of entropy over the system boundary (Ψ˙ ) and generation of entropy within the system boundaries (S˙gen). This form of the second law is valid for all processes in closed systems. The entropy generation rate is positive, S˙gen > 0, for irreversible processes, and it vanishes, S˙gen = 0, in equilibrium, and for reversible processes, where the system is in equilibrium states at all times.
All real technical processes are somewhat irreversible, since friction and heat transfer cannot be avoided. Reversible processes are idealizations that can be used to study the principle behavior of processes, and best performance limits.
Since a closed system can only be manipulated through the exchange of heat and work with the surroundings, the transfer of any other property, including the transfer of entropy, must be related to heat and work, and must vanish when heat and work vanish. Therefore the entropy flux Ψ˙ only be of the form
with coefficients β, γ that must be related to system and process properties.
Equation (4.2) gives the mathematical formulation of the trend to equilibrium for a non-isolated closed system (exchange of heat and work, but not of mass). The next step is to identify entropy S and the coefficients β, γ in the entropy flux Ψ˙ in terms of quantities we can measure or control.
Entropy in Equilibrium
For quasi-static processes, which are in equilibrium states at all times, the entropy generation vanishes, S˙gen = 0, and the equation (4.2) for entropy becomes
This equation relates entropy S to the state properties U and V , and implies that S (U, V ) is a state property as well. Since pressure p, volume V , temperature T , and internal energy U are related through the thermal and caloric equations of state, p = p (T, V ), U = U (T, V ), the knowledge of any two of these determines the others. Thus, entropy, our new property, can be written as a function of any two of the above properties, e.g., S (T, V ) or S (p, T ) or S (U, p) or S (U, V ). From the last form, we compute the time derivative of entropy with the chain rule,
So far, entropy and the coefficients β and γ in the entropy flux are not yet fixed. Since entropy is a state property, also its derivatives are state properties, and it follows that β and (β − γ) are state properties as well.1 Since S, U and V are extensive, their quotients and derivatives must be intensive quantities; therefore β and γ are intensive quantities. Obviously, we are interested in non-trivial entropy functions, and therefore we must have β j= 0, (β − γ) j= 0.
In anticipation of later discussion we introduce the thermodynamic temperature as T = 1/β. At this point, this is a just a definition, however, it will be shown soon that T has all the characteristics required for the definition of a thermodynamic temperature. In particular, it will be seen that the entropy flux term βQ˙
= Q˙ /T is related to the restriction of the direction of heat transfer: heat flows from warm to cold, not vice versa. No such restrictionapplies for work, which, by means of gears and levers, can be transmitted from slow to fast and vice versa, or from low force to high force and vice versa. Because of this, γ must be a constant, which can be set to γ = 0—the interested reader will find the full argument in Sec. 4.17.
With β = 1/T and γ = 0, we have the partial derivatives of entropy expressed through measurable quantities,