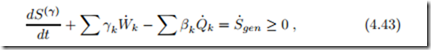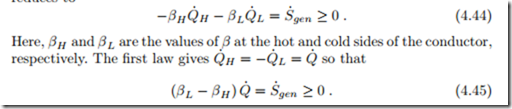Entropy and Disorder
Often it is said that entropy is a measure for disorder, where disorder has a higher entropy. This can be related to the above discussion by means of the following analogy: The ordered state of an office is the state where all papers, folders, books and pens are in their designated shelf space. Thus, they are confined to a relatively small initial volume of the shelf, V1. When work is done in the office, all these papers, folders, books and pens are removed from their initial location, and, after they are used, are dropped somewhere in the office—now they are only confined to the large volume of the office, V2. The actions of the person working in the office constantly change the microstate of the office (the precise location of that pen . . . where is it now?), in analogy to thermal motion.
At the end of the day, the office looks like a mess and needs work to clean up. Note, however, that the final state of the office—which appears to be so disorderly—is just one accessible microstate, and therefore it has the same probability as the fully ordered state, where each book and folder is at its designated place on the shelf. A single microstate, e.g., a particular distribution of office material over the office in the evening, has no entropy. Entropy is a macroscopic property that counts the number of all possible microstates, e.g., all possible distributions of office material.
A macroscopic state which puts strong restrictions on the elements has a low entropy, e.g., when all office material is in shelves behind locked doors. When the restrictions are removed—the doors are unlocked—the number of possible distributions grows, and so does entropy. Thermal motion leads to a constant change of the distribution within the inherent restrictions.
To our eye more restricted macroscopic states—all gas particles only in a small part of the container, or all office material behind closed doors—appear more orderly, while less restricted states generally appear more disorderly. In this sense one can say that entropy is a measure for disorder.
In the office, every evening the disordered state differs from that of the previous day. Over time, one faces a multitude of disordered states, that is the disordered office has many realizations, and a large entropy. In the end, this makes cleaning up cumbersome, and time consuming.
Our discussion focussed on spatial distributions where the notion of or- der is well-aligned with our experience. The thermal contribution to entropy is related to the distribution of microscopic energy em over the particles, where em is the microscopic energy per particle. In Statistical Thermodynamics one finds that in equilibrium states the distribution of microscopic energies between particles is exponential, A exp fem . The factor A must be chosen such that the sum over all particles gives the internal energy, . One might say that the exponential itself is an orderly function, so that the equilibrium states are less disordered than non- equilibrium states. Moreover, for lower temperatures the exponential is more narrow, the microscopic particle energies are confined to lower values, and one might say that low temperature equilibrium states are more orderly than high temperature equilibria. And indeed, we find that entropy grows with temperature, that is colder systems have lower entropies.
Entropy and Life
Earth itself is not isolated, since it receives an abundance of high temperature energy from the sun in form of radiation (sun surface temperature TS rv 5700 K). At the same time Earth emits low temperature energy, also in form of radiation (Earth surface temperature TE rv 300 K). This exchange of energy with Earth’s surrounding allows decreasing entropy locally on the planet. When we assume that the amount of heat received and emitted by ra- diation is the same ( Q˙ ), the second law for Earth reads dS ≥ Q˙ − .
dt TS TE Since TS > TE , the left hand side is negative, Earth’s entropy may, but must not, decrease.
If entropy is decreasing within a system (which cannot be isolated!), entropy must be growing somewhere else. When a sufficient portion of the surroundings are included in the system, entropy must grow. The entropy in the universe, which is a rather large isolated system, is increasing. The processes in the sun create entropy locally, in the sun.
Life, most importantly, is fed by the sun. Just think of the human body: we grow, we learn, and thus keep disorder within the confines of our body rather small. As humans are open systems, we maintain a low entropy level by exchange of mass and energy with our surroundings. Within the larger system around us, entropy grows, but within the smaller boundaries of our bodies (and minds!), entropy decreases, or is at least maintained at the same level.
The sun is the source of life, since it provides the energy we need to lower entropy in our open system Earth, and in our open system human body. Evolution, as an increase of order, does not contradict the second law.
The Entropy Flux Revisited
When we discussed the possible form of the entropy flux Ψ˙ in Sec. 4.3, we introduced two coefficients β, γ but we soon set them to β = 1/T and γ = 0 in order to simplify the proceedings. In this section, we run briefly through the proper line of arguments that show that γ must be a constant, which can be set to zero. The argument also shows that β must depend only on temperature, must grow inversely to temperature, and must be positive. Thus β behaves like inverse thermodynamic temperature, which agrees with our statements above.
For the argument we split the inhomogeneous system under consideration into a large number of small subsystems, each with their individual properties, see Fig. 4.3. With the entropy flux Ψ˙ = βQ˙ − γW˙ we find the second law for non-equilibrium systems from summing over subsystems as
where S(γ) is the entropy for this choice of flux. As before, Q˙ k , W˙ k denote the exchange of heat and work with the surroundings of the system, and βk , γk are the corresponding values of the unknown coefficients in the sub-systems at the system boundaries. All internal exchange of heat and work between the subsystems must be such that entropy is generated. The corresponding terms are absorbed in the entropy generation rate S˙gen. The first law for the system is given in (4.23).
We consider the above form (4.43) of the second law for a heat conductor.
For steady state heat transfer without any work exchange between a hot reservoir (H) and a cold reservoir (L) through the heat conductor, the above reduces to
Since heat must go from hot to cold, the heat must be positive, Q˙ > 0, which requires (βL − βH ) > 0. Thus, the coefficient β must be smaller for the part of the system which is in contact with the hotter reservoir. This must be so irrespective of the values of any other properties at the system boundaries (L, H). Therefore β must depend on temperature only.
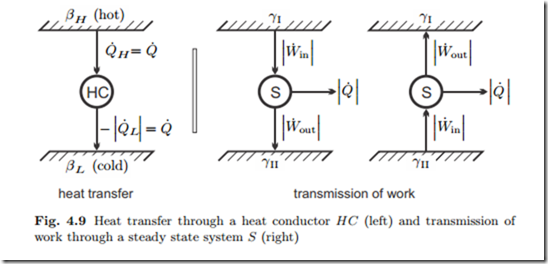
It follows that β must be a decreasing function of temperature alone, if temperature of hotter states is defined to be higher. The left part of Fig. 4.9 shows a schematic of the heat transfer process.
We proceed with the discussion of the coefficient γ. For this, we turn our attention to the transmission of work. The right part of Fig. 4.9 shows two “reservoirs” characterized by different values γI, γII between which work is transmitted by a steady state system S. The direction of work transfer is not restricted: by means of gears and levers work can be transmitted from low to high force and vice versa, and from low to high velocity and vice versa. Therefore, transmission might occur from I to II, and as well from II to I. Accordingly, there is no obvious interpretation of the coefficient γ.
Friction might occur in the transmission. Thus, in the transmission process we expect some work lost to frictional heating, therefore W˙ out ≤ W˙ in . In order to keep the transmission system at constant temperature, some heat must be removed. Work and heat for both cases are indicated in the figure, the arrows indicate the direction of transfer.
With S = S(γ) − γE as the standard entropy, and T = 1/ (β − γ) as the positive thermodynamic temperature, we find the second law in the form (4.24). This is equivalent to setting γ = 0, and β = 1/T as was done in Sec. 4.4.