The First Law of Thermodynamics:Exact and Inexact Diﬀerentials and Heat Transfer.

Exact and Inexact Diﬀerentials

Above we have seen that work depends on the process path. In the language of mathematics this implies that the work for an inﬁnitesimal step is not an exact diﬀerential, and that is why a Greek delta (δ) is used to denote the work for an inﬁnitesimal change as δW . As will be seen in the next section, heat is path dependent as well.

State properties like pressure, temperature, volume and energy describe the momentary state of the system, or, for inhomogeneous states, the momentary state in the local volume element. State properties have exact diﬀerentials for which we write, e.g., dE and dV . The energy change E2 −E1 = [ dE and the volume change V2 − V1 = [ 2 dV are independent of the path connecting the states.

It is important to remember that work and heat, as path functions, only describe property changes, not states. A state is characterized by state properties (pressure, temperature, etc.), it does not possess work or heat.

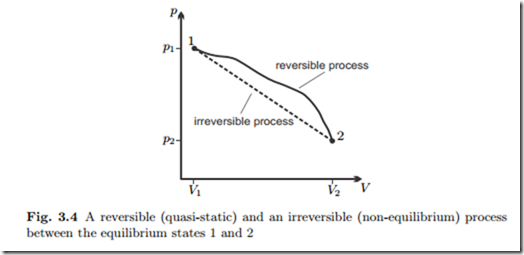
Quasi-static (reversible) processes go through well deﬁned equilibrium states, so that the whole process path can be indicated in diagrams, e.g., the p-V-diagram.

Non-equilibrium (irreversible) processes, for which typically the states are diﬀerent in all volume elements, cannot be drawn into diagrams. Often irreversible processes connect homogeneous equilibrium states which can be indicated in the diagram. We shall use dashed lines to indicate non-equilibrium processes that connect equilibrium states. As an example, Fig. 3.4 shows a p-V-diagram of two processes, one reversible, one irreversible, between the same equilibrium states 1 and 2. We emphasize that the dashed line does not refer to actual states of the system. The corresponding work for the non equilibrium process cannot be indicated as the area below the curve, since its computation requires the knowledge of the—inhomogeneous!—pressures at the piston surface at all times during the process.

Heat Transfer

Heat is the transfer of energy due to diﬀerences in temperature. Experience shows that for systems in thermal contact the direction of heat transfer is restricted:

Heat will always go from hot to cold by itself, but not vice versa.

This restriction of direction is an important diﬀerence to energy transfer by work between systems in mechanical contact, which is not restricted.

Since heat ﬂows only in response to a temperature diﬀerence, a quasi-static (reversible) heat transfer process can only be realized in the limit of inﬁnitesimal temperature diﬀerences between the system and the system boundary, and for inﬁnitesimal temperature gradients within the system.

The main heat transfer mechanisms are: (a) Heat conduction, where thermal energy is transmitted by microscopic energy exchange between neighboring particles. (b) Convection, where ﬂuid elements move to hotter or colder parts of the system and then exchange energy with the new neighborhood.

(c) Radiative transfer, where electromagnetic radiation that crosses the system boundaries is absorbed or emitted by the matter inside the system. In the present context we do not need to discuss the details of these heat transfer mechanisms, which ultimately describe the same thing: energy transfer driven by temperature diﬀerence.

We use the following notation: Q˙

denotes the heat transfer rate, that is the amount of energy transferred as heat per unit time. Heat depends on the process path, so that the heat exchanged for an inﬁnitesimal process step, δQ = Q˙ dt, is not an exact diﬀerential. The total heat transfer for a process between states 1 and 2 is

By convention, heat transferred into the system is positive, heat transferred out of the system is negative.

A process in which no heat transfer takes place, Q˙ = 0, is called adiabatic process.

In general, there might be several heat interactions Q˙ k of the system, then the total heat for the system is the sum over all contributions; e.g., for the heating rate

Confusion might result between the use of the word heat in everyday language, and its use in thermodynamics. In thermodynamics, heat solely de- scribes a means to transfer energy in response to temperature diﬀerences. In particular we emphasize that heat is not a form of energy, and does not relate to how hot it might be outside. To say “oh, what a heat” is common language, a thermodynamicist will say “oh, it’s pretty hot outside”, or, even better, “oh, the temperature is pretty high today.” A state is characterized by its energy or temperature, a change of state is characterized by heat (transfer).