Heat Transmission Loss Formula
The heat loss (expressed in Btu) of a given space is determined by multiplying the coefficient of heat transmission by the area in square feet by the design temperature difference (i.e., the difference between the indoor and the outdoor design temperatures). Because a heating system must supply an amount of heat equal to the amount of heat lost in order to maintain a constant indoor design temperature, heat loss is approximately equal to heat required. This may be expressed by the following formula:
Ht = AU (ti – to) where Ht = heat loss transmitted through a structural section (e.g., roof, floor, ceiling) expressed in Btu per hour, representing both the heat lost and the heat required.
A = area of structural components in square feet.
U = overall coefficient of heat transmission.
To = outdoor design temperature.
Ti = indoor design temperature.
Computing Total Heat Loss
The commonly accepted procedure for calculating the total heat loss from a structure is to calculate the heat loss for each room or space separately and then add the totals.
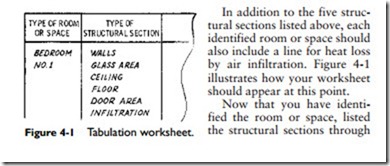
The heat loss calculation worksheet you use should contain a column in which each room or space can be identified separately. Under the identification are listed those structural sections through which heat transmission losses occur. When applicable, these will include all or most of the following:
1. Walls
2. Glass
3. Ceiling
4. Floor
5. Door(s)
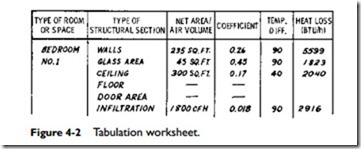
which heat loss occurs, and calculated the rate of air infiltration, you must determine the net surface area and the U-value for each structural section. The design temperature difference must also be determined and entered for each structural section. Except where surfaces are exposed to partially heated spaces (e.g., a garage, attic, or basement), each structural section will have the same design temperature difference. An example of how your worksheet should look at this point is illustrated in Figure 4-2.
Each identified room or space should also include the calculated air infiltration heat loss (see Infiltration Heat Loss following). The amount of heat loss due to air infiltration will depend upon the size, type, and number of windows and doors and other variables.
The bedroom given as an example in Figure 4-1 has two exposed walls (8 ft X 15 ft and 8 ft X 20 ft). The number of air changes suggested for a room with two exposed walls is 11⁄2 changes per hour.
The volume of air infiltration for the bedroom can be calculated as follows:
The total heat loss for bedroom No. 1 (as it would be designated on the worksheet) is 12,378 Btu/h. If there is a door in one of the outside walls, its heat loss also has to be calculated and entered on the worksheet. Furthermore, the door area (in square feet) would have to be subtracted from the surface area for the walls, because the latter is always a net figure.
After calculating the heat loss for each room or space in the structure, the results are added to obtain the total heat loss (in Btu/h) for the structure.
Loss in Doors and Windows
It is not easy to compute the coefficient of heat transmission (U-value) for a door because door construction varies considerably in size, thickness, and material. A fairly accurate rule-of-thumb method is to use the U-value for a comparable size single-pane glass window. If you wish to compute the coefficient of heat transmission for a door, the necessary data can be found in ASHRAE publications. The same source can be used for computing the coefficients of heat transmission of windows.
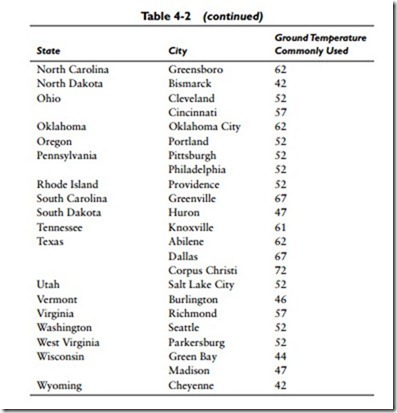
Loss in Basements
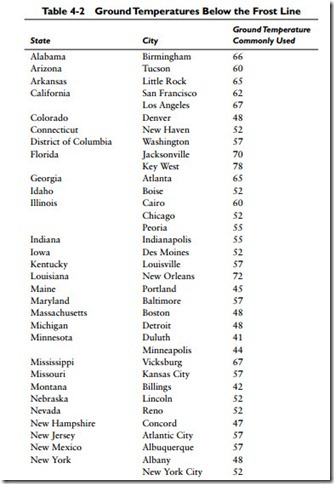
The amount of heat lost from a basement will depend upon a number of different variables. An important consideration, for example, is ground temperature, which will function as the outdoor design temperature in the heat loss transmission formula. The ground temperature will vary with geographical location (Table 4-2).
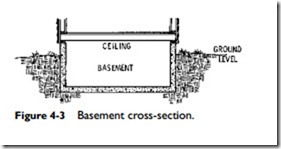
The usual method for calculating heat loss transmission through basement walls is to view them as being divided into two sections (Figure 4-3). The upper section extends from the frost line to the basement ceiling and includes those portions of the wall exposed to outdoor air temperatures. The heat loss for this section of the basement wall is calculated in the same way that other surfaces exposed to the outside air are calculated. The section of the wall extending
from the frost line to the basement floor and the floor itself can be calculated on the basis of the ground temperature. The ground temperature is substituted for the outside design temperature when calculating heat loss.