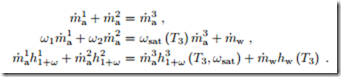Evaporative Cooling
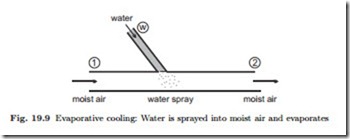
Next we consider cooling and moisturizing of air by addition of liquid water, again by means of an example, see Fig. 19.9. The initial state is relatively dry air at a pressure of p = 1 bar, relative humidity φ1 = 0.2, and temperature T1 = 40 ◦C, so that ω1 = 0.009. Liquid water at Tw = 20 ◦C is sprayed into
the air, and we ask how much liquid must be added per kg of air in order to lower the temperature to T2 = 30 ◦C. The conservation laws for water mass and energy for this process read
This almost agrees with the expression (19.16), the only difference is the value of the temperature of the added water in the denominator. If the added liquid water in (19.16) is at the wet-bulb temperature of state 1, then the wet-bulb temperature will stay constant. Since under HVAC conditions the enthalpy of the vapor exceeds the enthalpy of the added liquid by far, the denominators in (19.16) and (19.18) will be very close, and both equations will give almost the same result.
In short, evaporative cooling, that is injection of liquid water into moist air, can be well approximated as a process of constant wet-bulb temperature. The psychrometric chart shows lines of constant Twb and can be used to evaluate these processes. Moreover, since the lines of constant enthalpy h1+ω are almost parallel to the lines of constant wet-bulb temperature, some authors suggest to describe evaporative cooling as a constant enthalpy process.
Adiabatic Mixing
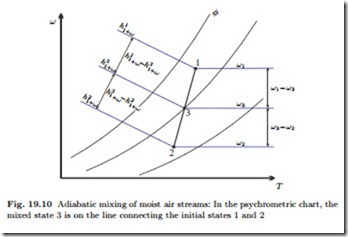
We consider the adiabatic and isobaric mixing of two moist air streams of states 1 and 2. Mass and energy balances relate the final state 3 to the incoming streams as
A special situation may arise due to the convexity of the saturation line (φ = 1). It can happen that the line connecting the two initial states lies outside the accessible region of the diagram. Figure 19.11 shows this for the special case of mixing of two saturated states. In these cases, some liquid water will fall-out as fog, and the mixture will be in the saturated state. Obviously, formation of fog must be avoided in HVAC applications. The relevant equations are again the conservation laws for air and vapor mass, and for energy, which now read
Due to the occurrence of ωsat (T3), these are three non-linear equations for the three unknowns T3, m˙ w, m˙ 3, which are best solved numerically.
The air on top of water bodies normally is saturated. When two streams of water at different temperatures meet, fog will occur as a result of the mixing of the two accompanying air flows.