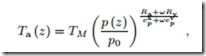Problems
Compression of Moist Air
Air initially at 1 atm, 25 ◦C and relative humidity of 60% is compressed isothermally until condensation of water occurs. Determine the pressure at the onset of condensation. Draw the process for the vapor into a T-s-diagram.
Compressed Air
To avoid condensation of water in compressed air lines, it might be necessary to dehumidify the compressed air. To study this, consider a compressor that draws outside air at 93 kPa, 14 ◦C and relative humidity of 40%, and compresses it to 800 kPa. After compression, the air flows through ducts for distribution, where it is cooled to the workshop temperature of 22 ◦C. Deter- mine the dewpoint of the compressed air–will there be condensation in the pipes?
Air Conditioning
An air conditioning system provides a volume flow of 3 m of moist air at 1 atm, 22 ◦C and 50% relative humidity by conditioning outside air at 34 ◦C and 50% relative humidity. For this, the outside air is first cooled and dehumidified, and then heated to the final temperature. Assume that the condensate leaves the system at 10 ◦C and determine the temperature after dehumidification is completed, the amount of heat that must be withdrawn in the cooling process, and the heat added in the heating process per unit mass of dry air.
Air Conditioning
An air conditioning system provides air at 1 atm, 20 ◦C and 60% relative humidity which is obtained from outside air at 38 ◦C and 70% relative humidity as follows: The outside air is first cooled and dehumidified, and then heated to the desired final temperature. The pressure stays constant throughout the process. Determine the temperature after dehumidification is completed, and assume that the condensate leaves the system at this temperature. Next, de- termine the heat that must be withdrawn in the cooling process, and the heat added in the heating process, both per unit mass of dry air. Finally, determine the mass flow and the volume flow of the air delivered, when the cooling power of the system is 150 kW.
Humidification
An air conditioning system draws 22 m outside air at 1 atm, 10 ◦C and 40% relative humidity. The air is first heated to 22 ◦C, and then humidified by injection of steam. The air leaves the system at 25 ◦C and 55% relative humidity. Determine the rate of heat supply in the heating section, the mass flow rate of steam required, and the temperature of the steam.
Humidification
At an elevated location, an air conditioning system draws 20 m outside air at 0.8 bar. With a psychrometer it is determined that the dry- and wet- bulb temperatures of the incoming air are 10 ◦C and 2.5 ◦C, respectively. To reach the desired state, the air is first heated to a temperature T2, and then humidified by injection of superheated steam at 0.8 bar, 150 ◦C, where the enthalpy is 2777.84 kJ . The air leaves the system at 22 ◦C and 55% relative humidity. Determine the mass flow rate of steam required, the rate of heat supply in the heating section, and the temperature of the air before steam is injected.
Dehumidification and Mixing
The outside air of a building is at 26 ◦C, and 90% relative humidity, the pressure is 1 atm. The air conditioning system of the building is required to provide air at 22 ◦C and 50% relative humidity. To reach that state, the flow of incoming outside air is split into two streams.
One stream is dehumidified by cooling to 5 ◦C so that liquid water condenses, and subsequent reheating. The cooling system removes 6 kW from this flow.
Then, the dehumidified stream is mixed with the other stream, so that the desired state is reached.
For the solution use the psychrometric chart.
1. Determine the dry air mass flows of the two streams.
2. Determine the heat required for the reheating of the dehumidified stream.
3. The final air flow should not be faster than 3 m , determine the cross section of the duct.
Air Conditioning
An air conditioning system draws a volume flow of 20 m of outside air at 30 ◦C and 90% relative humidity (state 1). The air flow is divided in to two streams, stream A and stream B. Stream A is first dehumidified by cooling to 5 ◦C (state 2), and then heated to state 3. Stream A and stream B are then mixed adiabatically. The mixture has a dry-bulb temperature of 20 ◦C at 50% relative humidity (state 4). The pressure is constant at 1 atm throughout the process.
1. Indicate the states 1,2,3,4 in the psychrometric chart.
2. Compute the ratios of dry air mass flows , and the values of the two mass flows.
3. Compute the heat to be removed from (1-2) and added to (2-3) stream A.
4. Is it feasible to do both, heating and cooling with a single refrigeration cycle? Discuss?
Evaporative Cooling
To provide air at a desired state, a volume flow of 10 m outside air (dry-bulb temperature 15 ◦C, wet-bulb temperature 10.8 ◦C) is first heated to 30 ◦C and then cooled and humidified by spraying of liquid water. The final temperature is 25 ◦C. Determine the relative humidity at the exit, the mass flow of water added, and the heating rate required. Use the psychrometric chart.
Evaporative Cooling
An air conditioning system draws a volume flow of 50 m of outside air at 40 ◦C and 10% relative humidity (state 1). To produce moist air of pleasant conditions, this air is first cooled by evaporative cooling to state 2, and then by heat exchange with a cooling system to the final state, with dry-bulb temperature T3 = 20 ◦C at φ3 = 60% relative humidity. The pressure is constant at 1 atm throughout the process.
1. Indicate the states 1,2,3 in the attached psychrometric chart.
2. Determine the mass flow of water required for evaporative cooling (1-2).
3. Determine the heat to be removed, Q˙ 23, in kilowatts.
4. A leak occurs in the system, and moist air at state 3 is mixed with outside air. Determine the dry air mass flow of leaked air when the mixture has a dry-bulb temperature of T4 = 22 ◦C.
Mixing of Two Moist Air Streams
Consider the adiabatic mixing of two streams of moist air at p = 1 atm.
Stream 1 is saturated moist air of 20 ◦C at a volumetric flow rate of 60 m and stream 2 is moist air of 34 ◦C, 20% relative humidity. The relative humidity after mixing is 60%. Mark all relevant points on the psychrometric chart.
1. For the incoming flows and for the mixture, determine the values for enthalpy, temperature, relative humidity, humidity ratio, and specific volume.
2. Determine the dewpoint temperature and the wet-bulb temperature of the mixture
3. Compute the volumetric flow of stream 2.
Mixing of Air Streams
Two streams of moist air are mixed adiabatically at 1 atm. One stream has a dry-bulb temperature of 40 ◦C and a wet-bulb temperature of 32 ◦C, and the mass flow rate is 8 kg . The other stream is saturated air at 18 ◦C with a mass flow rate of 6 kg . Determine the state of the mixture (temperature, specific humidity, relative humidity, enthalpy, volume flow).
Air Conditioning in the Desert
In the desert: The outside air of a building is at 40oC, and 10% relative humidity, the pressure is 1 atm. The air conditioning system of the building is required to provide air at 20 ◦C and 50% relative humidity. To reach that state, the flow of incoming outside air is split into two streams, A and B:
Stream A is spray-cooled by injection of liquid water to a relative humidity of 100%, the mass flow of water (at 20 ◦C) injected is 10 kg .
Stream B is cooled to temperature TB by a standard refrigeration cycle with COP of 3. Then, the spray-cooled stream A is mixed with stream B, so that the desired end state is reached.
1. Make a sketch of the process, and enter the relevant points in the psychrometric chart.
2. Determine the temperature TB .
3. Determine the dry air mass flows of both streams.
4. Determine the heat removed from stream B, and the power requirement of the refrigerator.
Cooling Tower
In a 500 MW steam power plant, the condenser is cooled by a cooling water flow that enters the condenser at 26 ◦C, and leaves at 40 ◦C. The cooling water is cooled back to 26 ◦C in a natural-draft cooling tower which draws environmental air at 1 atm with dry- and wet-bulb temperatures of 23 ◦C and 18 ◦C, respectively, and discharges saturated air at 37 ◦C. The thermal efficiency of the power plant is 43.5%. Determine mass flow of cooling water, volume flows of air into and out of the cooling tower, and the required mass flow of makeup water.
Clouds
Cumulus clouds are formed when air at the ground is heated, takes up moisture, and then rises due to its buoyancy. While rising, the moist air expands, more or less adiabatically, since the pressure decreases with height. During expansion the temperature of the rising air is decreasing. When the temperature reaches the dew point temperature, water vapor condenses, and a cloud is formed.
In order to compute the height of the clouds, assume that the pressure in the atmosphere is given by the barometric formula 2.26.
Consider a fixed mass of moist air, that occupies a volume V , and has enthalpy H. Consider the moist air as an ideal gas, so that its enthalpy and volume are given as
Here, ma is the mass of dry air, ω is the humidity ratio, ca , cv and Ra, Rv are the specific heats and gas constants of dry air and vapor, hfg (TR) is the heat of evaporation of water at TR = 273.15 K, Ta is the temperature of the rising moist air, and p is the local pressure.
1. Discuss the assumptions behind the equations for enthalpy and volume.
2. Show that the first law for an adiabatic process for the moist air gives dH = V dp.
3. Show that the temperature of the rising moist air is given by
where TM is the temperature of the moist air at the ground, just before rising (at z = 0).
4. Employ the ideal gas law for the vapor to find its partial pressure in the moist air as
5. The saturation pressure for the vapor is given by psat (Ta (z)), and water will condense, when pv (z) > psat (Ta (z)). Set TM = 298 K, ω = 0.01 (or other values), and find the height zCloud, where clouds begin to form.