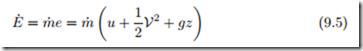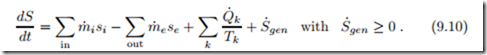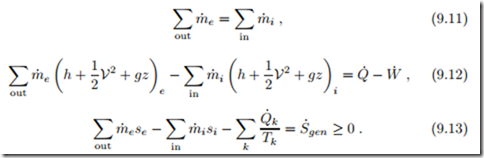Flows in Open Systems
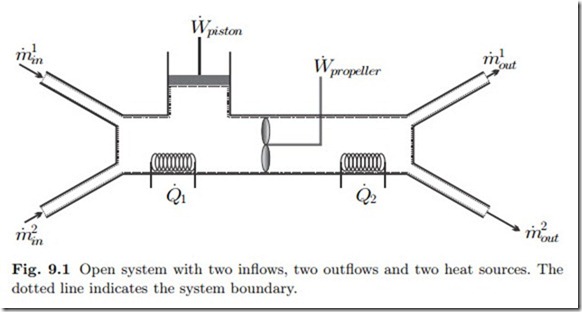
So far we have considered only closed systems, which do not exchange mass. We shall now extend the discussion to systems which exchange mass with their surroundings. Figure 9.1 shows a generic open system with two inflows and two outflows. In the following, and in the figure, the amount of mass exchanged per unit time, the mass transfer rate or mass flow, is denoted by m˙ . The system also exchanges propeller and piston work, W˙ = W˙ propeller + W˙ piston, and heat, Q˙ = Q˙ 1 +Q˙ 2, with its surroundings, just as a closed system does. Below, we shall add the appropriate terms to the thermodynamic laws to account for mass transport over the system boundary.
States in open systems are normally inhomogeneous. One might think of a mass element entering the system of Fig. 9.1 on the left. As the element of mass travels through the system, it constantly changes its state: When it passes the heating, its temperature changes, when it passes the propeller its
pressure and temperature change and so on. Thus, at each location within the system one finds different properties. As discussed earlier, an inhomogeneous system is in a non-equilibrium state. In an open system the non-equilibrium is maintained through the exchange of mass, heat and work with the surroundings.
Conservation of Mass
Mass cannot be created or destroyed, that is mass is conserved. Chemical reactions change the composition of the material, but not its mass.1 In a closed system, the law of mass conservation states that the total mass m in the system does not change in time, i.e., it simply reads dm = 0. In an open system, where mass enters or leaves over the system boundaries, the conservation law for mass states that the change of mass in time is due to inflow—which increases mass—and outflow—which decreases system mass. In other words, the rate of change in mass is due to the net difference of mass flows entering and leaving the system,
Here, m˙ i denotes incoming mass flows and m˙ e denotes exiting mass flows, as indicated in Fig. 9.1. By definition, the mass flow is positive, the direction of flow is made explicit by the signs in the equation.
Figure 9.2 shows an element dA of the system boundary that is crossed by mass flowing with the local velocity V⊥. All velocity components parallel to the surface do not play a role in transport through the surface elements, and it suffices to consider only the normal (i.e., perpendicular to dA) velocity V⊥ as indicated in the figure. During the time interval dt a mass element travels the distance ds = V⊥dt. All mass elements that are initially in the volume element dsdA = V⊥ dA dt will cross the surface element dA during dt. With the local density ρ, the mass in the volume element is ρV⊥ dA dt, which thus is the mass crossing dA during dt. Division by the time interval dt gives the amount of mass crossing the surface element per unit time as ρV⊥ dA. The macroscopic mass flow through a finite cross section A results from integration over all surface elements,
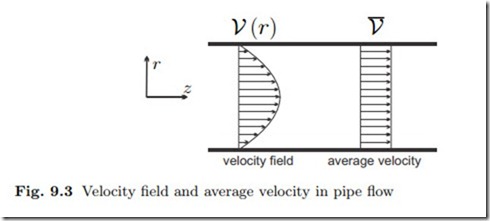
For a finite cross section one will expect spatial variations of the density ρ and velocity V⊥ over the cross section which would have to be taken into account in the integral. As an example Fig. 9.3 shows a typical velocity profile in pipe flow, where the fluid sticks to the wall, so that the velocity at the wall is zero, and the flow is fastest in the middle. However, for many engineering applications it is not necessary to resolve the velocity profile, or the profiles of other properties. Instead, it suffices to work with local averages, and this will be done from now on. When the average values are inserted in (9.2), they can be pulled out of the integral, and we find
where ρ and V are averages over the cross section A.
Sometimes it is convenient to use the volume flow V˙
Flow Work and Energy Transfer
The total energy E of an open system changes due to exchange of heat and work, and due to convective energy transport, that is energy carried in or out by the mass crossing the system boundary. Apart from propeller and volume change work one has also to account for flow work, which is the work required to push mass over the system boundaries.
We consider convective transfer first: The specific energy e = u + 1 V2 + gz is the local energy per unit mass. Any element of mass crossing the boundary carries this specific energy along, and thus a mass flow m˙ tive energy
flux carries the convec over the system boundary.
Now we compute flow work. The power required to push mass over the system boundary is, as always, the force required times the velocity. The force is the local pressure times the cross section, thus
Work is done to the system when mass is entering, then W˙ flow must be negative. The system does work to push leaving mass out, then W˙ flow must be positive. Accordingly, flow work points opposite to mass flow, which is ensured by the minus sign in the equation.
Thus, in comparison to the energy balance for closed systems, the energy balance for the general open system of Fig. 9.1 has additional contributions to account for convective energy transport and flow work. In condensed notation it reads
The indices (i, e) indicate the values of the properties at the location where the respective flows cross the system boundary, that is their average values at the inlets and outlets, respectively. This equation states that the energy E within the system changes due to convective inflow and outflow, as well as due to heat transfer and work. Note that the flow energy includes the work required to move the mass across the boundaries (flow work). Moreover, there can be several contributions to work and heat transfer, that is W˙ = ),j W˙ j and Q˙ = ), Q˙ k .
Entropy Transfer
All mass that is entering or leaving the system carries entropy. The entropy flow associated with a mass flow is simply S˙ = m˙ s, where s is the specific entropy. Adding the appropriate terms for inflow and outflow to the 2nd law (4.24) for closed systems yields the 2nd law—the balance of entropy—for open systems as
This equation states that the entropy S within the system changes due to convective inflow and outflow, as well as due to entropy transfer caused by heat transfer (Q˙ k /Tk) and entropy generation due to irreversible processes inside the system (S˙gen ≥ 0). If all processes within the system are reversible, the entropy generation vanishes (S˙gen = 0). Recall that Q˙ k is the heat that crosses the system boundary where the boundary temperature is Tk .
Open Systems in Steady State Processes
Many thermodynamic systems and cycles are composed of open system de- vices. Since the cycles (e.g., power plants or refrigerators) run continuously, they are mainly operating at steady state. In the following sections we shall study the basic equations for steady open systems, and tabulate work and heat for the most important devices.
In steady state processes no changes occur over time at a given location.
Then all time derivatives vanish and mass balance (9.1), energy balance (9.9), and entropy balance (9.10) assume the forms
The interpretation of these equations is straightforward: The mass balance (9.11) states that, in steady state, as much mass leaves the system as enters. The energy balance (9.12) states that a change of the flow energy m˙ (h + 1 V2 + gz) between outflow and inflow is effected by exchange of heat and work. The last equation, Eq. (9.13), states that the difference of entropy flowing in and out of the system is due to transfer of entropy caused by heat transfer (Q˙ /T ) and entropy generation inside the system (S˙gen). Entropy is
created, if the processes are irreversible (S˙gen > 0), and entropy is conserved when all processes are reversible (S˙gen = 0).
Note that in a steady state process the volume of the system must remain unchanged, which implies that no piston work occurs: all work exchange is due to propeller work.