Osmosis and Osmotic Pressure
The word “osmosis” comes from the greek word for pushing and refers to the passing of a substance through a semi-permeable membrane. Applications are, e.g., cell membranes in the human body, or membranes for desalination. For the discussion of osmotic phenomena we shall assume ideal mixtures only.
The osmotic pressure is the pressure on the membrane due to those components of the mixture that cannot pass. Specifically, we consider a membrane which separates the pure solvent ν at pressure pps from an ideal mixture at pressure ps, see Fig. 21.1. The osmotic pressure is defined as the pressure difference over the membrane in equilibrium,
For the pure solvent, the chemical potential is just the specific Gibbs free energy, and we find by Taylor expansion
Recall that solutions of salt in water are not ideal mixtures, unless they are diluted, see Sec. 18.14.
Osmotic Pressure for Dilute Solutions
The osmotic pressure assumes a rather interesting form in the limit of dilute solutions, where most of the solution is solvent ν, that is nν » nα holds. Then we can expand
The dissolved substances in a dilute solution exert an ideal gas pressure on the membrane; the osmotic pressure is the sum of these ideal gas pressures.
Example: Pfeffer Tube
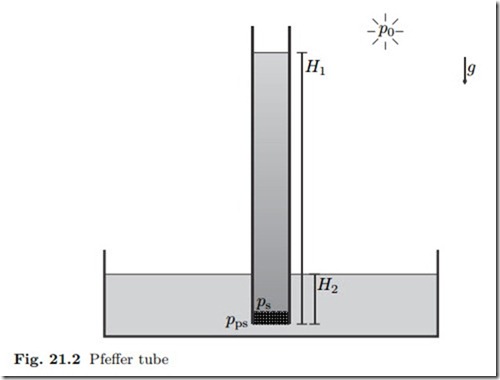
An instructive example for the strength of the osmotic forces is the Pfeffer tube (Wilhelm Pfeffer, 1845-1920), depicted in Fig. 21.2. The solvent is water. A tube is closed by a membrane that only lets the solvent ν pass, and is set vertically into a bath of solvent. Some solvent will pass the membrane, so that the solvent inside and outside the tube are at the same level. Then salt is added to the tube. This leads to an additional amount of solvent drawn from the bath into the tube; in the final equilibrium, the osmotic pressure and the hydrostatic pressure are balanced.
Since this is a system in which temperature and (environmental) pressure are controlled, the total Gibbs free energy G = H − TS + Epot of the system will minimize. Drawing solvent into the tube increases the entropy of the
dissolved particles, which now have a greater volume to access, but also in- creases the potential energy. The final equilibrium state, a balance of height increasing entropic force and height reducing energetic force, will be calculated next under some simplifying assumptions. The goal is the computation of the height H1 in the tube.
Directly at the membrane, the hydrostatic pressures of the solution in the tube and solvent in the bath are
When the tube is immersed into the pure solvent by H2 = 1 cm, the solution in the tube will reach a height of H1 = 9.29 m, which corresponds to about 1 litre of water in the tube! This shows the enormous forces that are present in osmosis, which are due to the desire of the salt to increase the entropy of mixing by making the accessible volume (i.e., the volume of the solution), as large as possible.
Due to the difference in density between salt solution and pure water, the height H1 becomes smaller as the tube is pushed deeper into the solvent (i.e., for larger H2), as the problems show, it might even happen that H2 > H1.
The strong desire of the salt to draw water can be used (and was widely used in the past) to cure meat: While water can pass cell membranes, salt cannot, and thus a piece of meat or fish immersed in salt will be depleted from some water. The same is true for bacteria on the meat which will die from dehydration, and thus cannot spoil the meat.
Since seawater contains more salt than the cells of the human body, drinking seawater is deadly: The seawater will draw water from the cells, which will be damaged by dehydration. In fact, after drinking seawater one will be more thirsty than before.
Another example for osmotic forces is putting sugar on strawberries, which will draw water (juice) out of the strawberries that mixes with the sugar. The opposite can be seen when raisins are put into water: the sugar inside the raisin draws water in, and the raisin swells.