Hydrostatic thrust on curved surfaces.

Hydrostatic thrust on curved surfaces

As hydrostatic pressure acts perpendicularly to a surface, the integration of δF over the surface can be complicated. One method of determining the thrust on a curved surface is to project its area on flat vertical and horizontal surfaces, as shown by AB and DE, respectively, in Figure 22.12.

From equilibrium considerations, F = Fx and W = Fy and these thrusts must act through the centre of pressures of the respective vertical and horizontal planes. The resultant thrust can be obtained by adding Fx and FY vectorially, where W = weight of the fluid enclosed by the curved surface and the vertical projection lines to the free surface, and G = centre of gravity of W.

Buoyancy

The upward force exerted by the fluid on a body that is wholly or partially immersed in it is called the buoyancy of the body.

The stability of floating bodies

For most ships and boats the centre of buoyancy (B) of the vessel is usually below the vessels’ centre of gravity (G), as shown in Figure 22.13(a). When this vessel is subjected to a small angle of keel (θ), as shown in Figure 22.13(b), the centre of buoyancy moves to the position B′,

The metacentric height GM can be found by a simple inclining experiment, where a weight P is moved transversely a distance x, as shown in Figure 22.14.

He then carries out an inclining experiment, where he moves a mass of 50 kg through a transverse distance of 10 m across the yacht’s deck. In doing this, he finds that the resulting angle of keel, θ = 1°. What is the metacentric height (GM) and the posi- tion of the centre of gravity of the yacht above the keel, namely KG? Assume g = 9.81 m/s2.

Problem 14. A barge of length 30 m and width  8 m floats on an even keel at a depth of 3 m. What is the value of its buoyancy? Take density of water, ρ, as 1000 kg/m3 and g as 9.81 m/s2.

The displaced volume of the barge,

(a) Weight of two end plates,

V = 30 m × 8 m × 3 m = 720 m3.

From Section 22.4,

Problem 15. If the vertical centre of gravity of the barge in Problem 14 is 2 m above the keel, (i.e. KG = 2 m), what is the metacentric height of the barge?

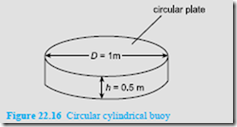
Problem 16. A circular cylindrical steel buoy, made from 10 mm thick steel plate, is of a hollow box-like disc shape, as shown in Figure 22.16. It is sealed off at its top and bottom by circular plates so that it is watertight. (a) If the external diameter of the buoy, D, is 1 m and its height, h, is 0.5 m, deter- mine its weight, W, given that the density of steel, ρS = 7860 kg/m3. (b) At what depth, H, will the buoy  float if the density of water, ρW = 1020 kg/m3?

(c) What is its GM? Take g to be 9.81 m/s2

Problem 17. A submarine pressure hull is in the form of a watertight circular cylindrical shell, of length 80 m, blocked off by flat ends, and of external diameter 10 m, and it descends to the bottom of the Mariana Trench, which is 11.52 km deep. What will be the hydrostatic pressure acting  on it? If a double-decker London bus is of mass 7 tonnes what will be the equivalent number of double-decker London buses acting on this hull?

Density of water, ρW = 1020 kg/m3. Take g to be  9.81 m/s2.

Practise Exercise 121 Further problems on hydrostatics

(In the following problems, where necessary, take g = 9.81 m/s2 and density of water ρ = 1020 kg/m3) 1. A ship is of mass 10000 kg. If the ship floats in the water, what is the value of its buoyancy? [98.1 kN] 2. A submarine may be assumed to be in the form of a circular cylinder of 10 m external diameter and of length 100 m. If the submarine floats just below the surface of the water, what is the value of its buoyancy? [78.59 MN]

3. A barge of length 20 m and of width 5 m floats on an even keel at a depth of 2 m. What is the value of its buoyancy? [2 MN]  = 115.27 MPa =  105 Pa/bar

4. An inclining experiment is carried out on the  = 1152.7 bar ≡ 1152.7 atmosphere (since 105 pascals = 1 bar ≡ 14.5 psi)  Let A = area of the external surface of the pressure hull  assuming flat ends = ð R 2 × 2 + 2ð RL  barge of Problem 3 where a mass of 20 kg is moved transversely across the deck by a distance of 2.2 m. The resulting angle of keel is 0.8°. Determine the metacentric height, GM.

[0.0155 m]

5. Determine the value of the radius of curvature of the centre of buoyancy, namely, BM, for the barge of Problems 3 and 4, and hence the position of the centre of gravity above the keel, KG. [2.026 m]

6. If the submarine of Problem 2 floats so that its top is 2 m above the water, determine the centre of curvature of the centre of buoyancy, BM. [0.633 m]

Incoming search terms:

• experimental method of determining metacentric height floating body
• thrust in curved surface
• thrust on curve surface
• thrust on curved