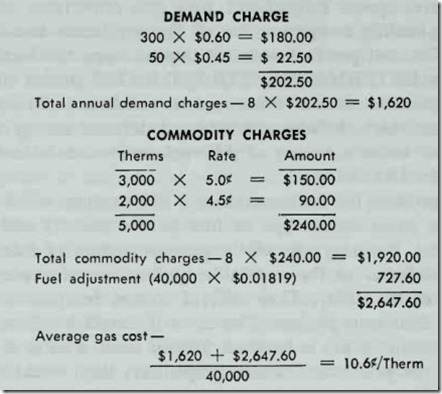THE DEGREE DAY FORMULA
The Degree Day Formula was devised some forty odd years ago by the American Gas Association and other groups, and has since been revised (see pages 627-8 of the 1970 ASHRAEGuide) to reflect internal heat gains and the levels of insulation. The correction factors involved in the revision are given in Tables 10 and 11. These correction factors should also be applied to the Corrected Heat Loss Formula (see the appropriate section in this chapter).
The Degree Day Formula is based on the assumption that heat for the interior of a house or building will be obtained from sources other than the heating system (e.g. sunlight, body heat of the occupants, etc.) until the outside temperature declines to
Table 10. Unit fuel consumption per degree day per 1000 Btu’s design heat loss.
Table 11. Correction factors for outdoor design temperatures.
65°F. At this point the heating system begins to operate. The consumption of fuel will be directly proportionate to the difference between the 65op base temperature and the mean outdoor tem perature. In other words, three times as much fuel will be used when the mean outdoor temperature is 35°F than when it is 55°F. The mean outdoor temperature can be determined by taking the sum of the highest and lowest outside temperatures during a twenty-four hour period beginning at midnight and dividing it by two. Each degree in temperature below 65°F is regarded as one “degree day.”
The Degree Day Formula is applied by dividing the heat loss figure by 1000 and multiplying the result by the figure for the unit fuel consumption per degree day per 1000 Btu’s design heat loss, which, in turn, is multiplied by the total number of degree days in the heating season (calculated on a 65op base) and then by the correction factors given in Tables 10 and 11. The appli cation of this formula is illustrated in Table 12.
Table 12. Application of the degree day formula.
THE NEMA FORMULA
The NEMA Formula was created by the National Electric Manufacturers Association. A constant of 18.5 is commonly used in the formula and reflects the percentage of heat loss that must be replaced by the heating system during a 24 hour period. In other words, the heating system will provide heat 77 percent of the time during a 24 hour period ( 24 X 18.5), while other heat sources will supply heat the remaining 23 percent.
The NEMA Formula consists of dividing the heat loss by 3413 (the number of Btu’s per kWh), and multiplying this figure by the total annual number of degree days, which figure is then multiplied by the constant (usually 18.5). The resulting product is then divided by the difference between the indoor and outdoor temperatures. The application of the NEMA Formula is illustrated in Table 13.
A major criticism of this formula by distributors of oil and gas heating fuels is that the use of the Heat Loss Formula gives a much higher kWh consumption rate than using the NEMA Formula.
OTHER HEATING COSTS
Energy requirements for non-heating purposes are an im portant additional factor to be considered when estimating total fuel costs for a house or building. This non-heating energy is used to operate oil and gas burners, automatic washers and dryers, water heaters, stoves, refrigerators and the variety of other appliances and work-saving devices deemed so necessary for modern living.
Table 13. Application of the NEMA formula.
This non-heating energy is commonly electricity or gas. Electricity is used to operate thermostats and other automatic controls found in heating and cooling equipment; burners, water heaters; home laundry equipment; refrigerators; and blowers for air con ditioners to mention only a few. Much of this equipment (e.g. water heaters, home laundry equipment, etc.) is also designed to be operated in conjunction with gas. Each of these appliances consumes energy that will account for a certain percentage of the homeowner’s utility bill. This must be accounted for when esti mating the total fuel requirement and heating cost.
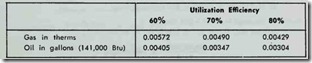
The most common method of determining which appliance is the most suitable one for a particular set of circumstances is by making a comparison of their energy use. For example, the esti mated usage for home laundry equipment (either a washer or a dryer) is one hour per week per occupant. In other words, a dryer would be operated five hours per week on the average in a household containing five people. For purposes of comparison, an electric clothes dryer draws 5.0 kW. per hour and a gas clothes
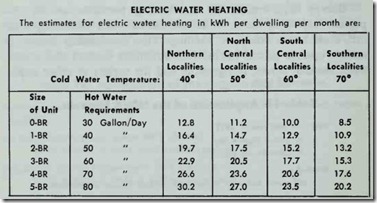
Table 14. Usage estimates for electric water heating.
(2) Demand. Where wholesale electricity is to be used for lighting, refrigeration, cooking, and domestic hot water, the monthly demand for all purposes may be estimated at 2.65 watts per kWh.
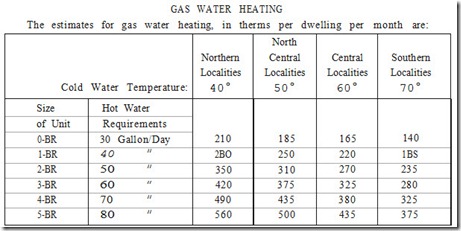
dryer uses approximately 3.5 therms of gas per month. Although these figures appear insignificant, they gain importance when the total non-heating energy use for all the appliances is added to gether. The cost per fuel unit will depend upon the local utility rates (see DETERMINING UTILITY RATES in this chapter). Some appliances, such as water heaters, will have to be compared on a basis which includes a number of different energy require ments met under a variety of different environmental conditions (see Tables 14 and 15).
The problem for the homeowner is to determine which type of appliance burns which type of fuel most efficiently and at the lowest cost. Probably one of the poorest sources of information is the distributor of the particular appliance or the rate corres pondent of the utility. They will, of course, be quite biased in favor of their own product. This is as it should be, because this is the reason they are in business. If they made a habit of recom mending the products of their competitors, they would soon be out of business.
Quite often consumer magazines will give the energy use rates of different appliances, and be quite frank in their comparison. This source is probably the most objective one to be found. How ever, knowing the rate at which an appliance consumes energy is only half the solution. It is also necessary to determine the utility rates.
Table 15. Usage estimates for gas water heating.
DETERMINING UTILITY RATES
No estimation of heating costs is complete until the utility rates for the various fuels available is determined and included in the estimate. Determining utility rates depends on so many variables that it, too, only serves as a cost estimation, not a pre cise figure . The problem is to arrive at as accurate an estimation as possible.
Among the many variables involved in determining utility rates are the following:
1. Differing rate structures,
2. Fuel/energy adjustment factors,
3. Variations in energy block sizes and prices,
4. Rate structure qualification procedures,
5. Community utility taxes,
6. Maximum demand charges.
Differing rate structures exist for different facilities or usage. The problem is to determine which rate structure will apply to the particular situation. This information can usually be obtained by contacting the local utility , and consulting with the utility rate correspondent.
Although this is a simplified explanation, a typical utility bill is computed by adding the demand charge, energy or commodity charge and the fuel adjustment charge, and dividing by the total amount of electricity or gas used during the billing period. This produces the average electric or gas cost. This procedure is illus trated in Table 16.