Free Energy & Exergy
⊳⊳⊳ Try It !! Look up “free energy” on the internet. No doubt you will find mostly conspiracy-theory web- sites, claiming that “free” (meaning ridiculously inexpensive) sources of energy are plentifully available—if only Big Oil (or whomever…) would just let us get our hands on it!
That is not the kind of free energy we will be talking about here—but then again, it is not entirely unrelated, either. There is, in fact, a great deal of energy all around us. Most of this is not free, however—in the sense of being available to perform work.
If the Second Law teaches anything, it is that it is impossible to convert all of a system’s internal energy into useful work. It is thus natural to define new thermodynamic quantities known as free energies—which represent that portion of U that is available to do work.”
What Would Happen If Entropy Were a Variable?
It all begins with the differential form of the First Law, Equation (8.1). Now that we also know about entropy, we can rewrite this [using Equation (10.1)] as
Equation (14.1) is remarkably simple and elegant. The right-hand side involves four quantities—each of which appears exactly once, three of which are known thermodynamic variables, and one of which is entropy.
⊳⊳⊳ To Ponder… When scientists see something simple and elegant like this, they call it “suggestive”—as if nature is revealing a sign or a hint…
In particular, Equation (14.1) seems to “scream” that S should be treated as a thermodynamic variable, not just a quantity. Indeed, treating U = U(S, V ) as a function of the two independent variables, S and V , Equation (14.1) becomes the total differential for U.
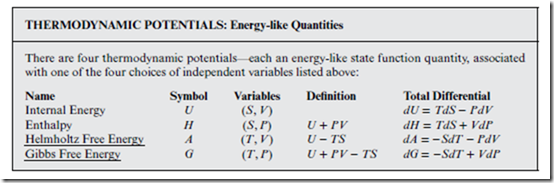
Henceforth, the set of thermodynamic variables is taken to be (T, S, P, V ), rather than (T, P, V ). Only two of these four variables are still independent, however, as can be seen clearly in the U(S, V ) example above.
The new picture nevertheless suggests a new choice of “natural” indepen- dent variables for U—i.e., (S, V ), rather than the (T, V ) set that has been used up till now (see Section 9.2). How do the natural variables change for the other thermodynamic quantities? Can we choose any two variables that we want, from our new set of four, to serve as independent variables? Looking more closely at Equation (14.1), it seems that the four variables come in two pairs: (T, S) and (P, V ). The two variables in each pair are called conjugate variables.
The last bullet in the box above implies that there are a total of four possible choices for the set of independent variables—namely: (S, V ); (S, P); (T, V ); (T, P). Uniquely associated with each of these four choices is a natural energy-like quantity—a so-called thermodynamic potential, obtained from U in similar fashion to the way that H was derived in Section 9.2. Specifically, the “trick” is to add (or subtract) conjugate pair products to U, in order to transform the natural variables appropriately.
Helmholtz and Gibbs Free Energies
Like enthalpy, the two new free energy quantities, A and G, serve as practical tools. They enable the Second Law to be applied directly to the system, rather than the total system—thus making it possible to forget about the surroundings entirely, and once again proving that It’s OK to be Lazy. This confers a great practical advantage in predicting which thermodynamic changes are spontaneous—but, as we will see shortly, only under certain conditions. As promised, the free energies also describe the extent to which the internal energy can be transformed into useful work.
Note that the total differential for every thermodynamic potential in the box above has the same elegant form as Equation (14.1)—all four variables appear exactly once, and in conjugate pairs. Whereas V is associated with U, and P with H, as was the case in Section 9.2, both U and H are now associated with S, rather than T. Transforming U and H into new quantities that depend naturally on T rather than S, one obtains A and G, respectively—which is another way to motivate the introduction of the latter.
Note also that A and G are obtained by subtracting the conjugate variable product TS from U and H (respectively), rather than adding it. This is a critical point; since all four variables are positive, free energy values are always less than the corresponding energies. To some extent, this reflects the Second Law fact that only some of the energy can be converted into useful work.
Since the independent variables (T, P) are generally preferred to (T , V ), G is more important than A, in practice. This is especially true for thermo- dynamic processes that occur at constant (T, P), such as phase transitions and chemical reactions (see Chapter 17 and the website). For this reason, we will often single out G for special treatment—even though similar analyses might hold for A, or even U and H.
For example, by comparing the total differential dG from the box above with Equation (9.16), we obtain the following elegant partial derivative relations:
Note the minus sign in front of the S in Equation (14.2) above—reflecting the idea that higher T leads to a greater entropic energy contribution that is “useless” for doing work.
Equation 14.2 also leads to an important partial derivative relation on the thermodynamic variables themselves—known as a Maxwell relation. Applying the cross-derivative trick of Section 9.4 [i.e., Equation (9.18)] to Equation (14.2),
There are four such Maxwell relations in all, one obtained from each thermodynamic potential.
⊳⊳⊳ Try It !! Try to derive all four Maxwell relations on your own, starting from each of the four thermodynamic potentials. Along the way, you will also derive six more partial derivative relations of the form of Equation (14.2). See also the Helpful Hint below.
Collectively, the set of four Maxwell relations describe the constraints imposed on the variables, (T, S, P, V )—by the fact that only two of these are independent. In this respect, they serve the same kind of role as the equation of state does for (T, P, V ).
⊳⊳⊳ Helpful Hint: Students are often asked to prove Maxwell relations. The first step is to confirm that the equation presented is a partial derivative relation involving only the four variables. The second step is to identify the two independent variables from the partial derivatives— e.g., T and P in Equation (14.3). The third step is to write down the total differential for the corresponding energy- like quantity, and to apply cross derivatives.
Second Law & Maximum Work
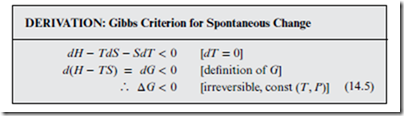
For a constant pressure change, dQ = dH by Equation (9.9), and so Equation (12.2) becomes
dH − TdS < 0. [irreversible, const P, infinitesimal] (14.4)
Assuming, also, that temperature is held constant, consider the following derivation:
Thus, the sign of ΔG of the system determines whether a process is spontaneous or not—provided that it takes place at constant (T , P). Likewise, if ΔG = 0, then the process is reversible. Similar relations hold for ΔA, for processes at constant (T, V ).
⊳⊳⊳ Helpful Hint: Make sure to get the direction correct, when working with the various inequalities derived from the Second Law. In particular, ΔG|T,P < 0—but ΔStot > 0—for a spontaneous irreversible change.
⊳⊳⊳ To Ponder… For a pure substance in a single phase (Section 3.1), the two variables (T, P) [or (T, V )] define the thermodynamic state—which therefore cannot change if both variables are held fixed. It is important to realize that Equation (14.5) [and also the ΔA analog] applies only to more complicated situations such as phase transitions and chemical reactions.
On the other hand, ΔA does say something important about gas expansions—provided that these occur at constant T. Specifically, ΔA is equal to the reversible, or maximum work that can be extracted from a true (ΔV > 0) isothermal gas expansion:
Figure 14.1 The path less traveled. Three travellers follow three different isother- mal paths from A to B: A. Lincoln (boots) takes the lower, irreversible path; M. Ghandi (bare feet) takes the middle, reversible path; E. Bunny (paw prints) takes the upper, irreversible path. The last path is not spontaneous and therefore forbid- den by the Second Law—the Easter Bunny doesn’t exist!
Figure 14.1 expands on the discussion at the end of Section 8.4, by offering additional insight as to why the reversible isothermal path provides maximum work. Any isothermal path lying above the reversible path would indeed generate more work; however, all such paths are nonspontaneous, and thus forbidden by the Second Law.
Note that directionality matters. For the reverse process—i.e., the B-to-A compression process—the upper irreversible path is spontaneous, and the lower irreversible path is forbidden. The reversible work now becomes the minimum work that must be applied to bring about the compression.
⊳⊳⊳ To Ponder… There is also a maximum non-expansion work principle, based on ΔG. This version requires constant (T, P)—and therefore only applies to more complicated situations, as per the To Ponder on p. 119. Examples include chemical reactions, and exergy (see below).
Exergy
From Section 13.2 we know that work can be generated whenever there is access to two heat baths at different temperatures—simply by sandwiching a heat engine in between them. This strategy succeeds because the heat is not transferred directly from the hot bath to the cold bath, but rather through an intermediary that is always at the same temperature as the bath it is in contact with. Even so, only some fraction of the absorbed heat is converted into work—a fraction that diminishes with the temperature difference, moreover.
This is important to know, because eventually, even large heat baths will thermally equilibrate with each other—once sufficient heat has been transferred via repeated heat engine cycles. In reality, the “isothermal” stages of the Carnot cycle are not truly so; because of heat transfer, each cycle reduces Th and increases Tc, however slightly—until eventually, Th = Tc, and no more work may be extracted. Useful work may also be obtained from two bodies that manifest a pressure difference—again, most efficiently through the agency of a reversible intermediary. Here, too, however, useful work ceases as soon as mechanical equilibrium of the two bodies is achieved.
In all then, how much useful work can be extracted before thermal and mechanical equilibrium are both reached? The theoretical maximum is known as the exergy, denoted ‘E’. Exergy is nearly equivalent to Gibbs free energy, as can be understood by considering the following important points:
1. Exergy requires three bodies, rather than two (system, surroundings, and intermediary.)
2. The intermediary enables a transfer of energy that is isothermal, isobaric, and reversible.
3. Under such conditions, ΔG is equal to the maximum useful or “non expansion” work.
Exergy can be formulated as follows. First, define the “system” to be the hot bath, rather than the intermediary (with T = Th, as per Section 13.2).
Second, take the (presumed) much larger cold bath to be the surroundings. Typically, the cold bath is the atmosphere, in which case Tc = T◦ and Pc = P◦ take on standard values. Consequently, T ◦ and P◦ remain effectively constant throughout the process, and useful work may be generated only until the system reaches T = T◦ and P = P◦—the so-called dead state.
Exergy is the useful work released by the total system, as the system progresses from its initial state to the dead state. Because of reversibility, ΔStot = Qtot = 0 (also, ΔVtot = 0). Because of the intermediary, however, the total system is not isolated, and so the useful work, Wtot = ΔUtot = E, is nonzero. Note that Wtot excludes the “useless” expansion work done on the surroundings by the system (or vice-versa), and is therefore equivalent to the “non-expansion” work.∗
The similarity between E and G is now obvious, as is the key difference— because of its dependence on T ◦ and P◦, exergy is a combined property that depends on both the system and the surroundings.
In practice, engineers also include other forms of energy in Equation (14.7), such as kinetic and potential energy of the system relative to the surroundings, chemical energy, electrical energy, etc. It may be that the exergy concept can be generalized still further.