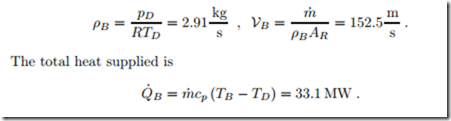Example: Ramjet
A ramjet is to fly at MaI = 3 in high altitude, where the temperature is TI = 200 K and the pressure is pI = 0.3 bar. The diffuser inlet, diffuser outlet, and nozzle inlet all have the cross section AR = 0.1 m2. We determine the throat cross sections of diffuser and nozzle, and the nozzle exit cross section for the case that the nozzle expands isentropically to the outside pressure. Moreover, we will compute exit velocity, thrust, and propulsive power. To simplify proceedings, we consider the working gas air as ideal gas with constant specific heats,![]()
Diffuser: The incoming flow is at TI , pI and MaI . The inlet density and velocity are
To be able to use the equations for nozzles, which also hold for diffusers, we first need to determine the stagnation state for the diffuser. The stagnation temperature TD0 follows from the first law (adiabatic deceleration), and the corresponding stagnation pressure pD0 follows from the isentropic relation
The diffuser exit area is given, and the corresponding exit pressure pD follows from the constant mass flow relation Aψ = const. by first determining the exit flow function ψD and then finding the corresponding pressure; this yields
The pressure can either be found from the plot of the flow function (Fig. 14.4), or by numerical solution of (14.28); note that there are two solutions, the larger one refers to subsonic flow. Temperature, density and velocity at the diffuser outlet are
Burner: In the burner, fuel is injected into the compressed air and isobarically burned. As always, we ignore the mass of the fuel added, and treat the combustion product as air. With the temperature after the burner at TB = 1300 K and the pressure pB = pD , we find density and velocity as
Nozzle: The inlet state for the nozzle is the exit state of the burner (ρB , TB , VB ). For the computation of the nozzle, we must first determine its stagnation state:
The computation of the throat cross section from critical data and the mass flow is already included in the above list.
The last process to consider is the isentropic expansion in the diverging part of the nozzle to the outside pressure pI = 0.3 bar. We find the following data for the nozzle exit:
Power and Efficiency: All cross sections and all property data for reversible operation were computed above. From the given data we find thrust and propulsive power as