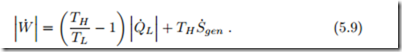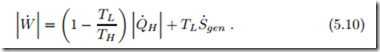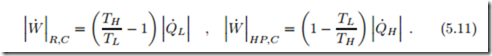Refrigerators and Heat Pumps
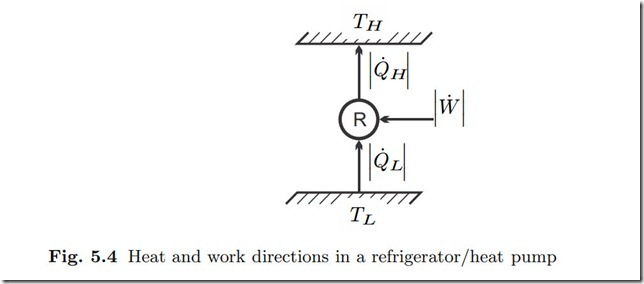
While heat cannot go from cold to warm by itself, one can use work consuming devices to perform this task, a refrigerator or heat pump as depicted in Fig. 5.4.
A refrigerator removes heat from a cold reservoir, e.g., the interior of a freezer, at TL, and rejects heat to the environment at TH —the goal is to cool the cold reservoir. A heat pump is used for space heating, it takes heat from the environment at TL, and rejects heat into the room that is being heated at TH . While the values of the temperatures TL, TH differ for refrigerator and heat pump, both operate according to the same principles.
With heat being removed from the colder reservoir, and heat rejected into the warm reservoir, we have ![]() combining first and second law by eliminating Q˙ H , we find the condition
combining first and second law by eliminating Q˙ H , we find the condition
This equation relates the work requirement, W˙ , to the heat removed from the colder reservoir, Q˙ L; it is well suited for evaluating refrigerators.
For heat pump systems one is interested in the work required in relation to the heat supply Q˙ H to the warmer reservoir. Eliminating Q˙ L one finds
Since T S˙gen ≥ 0, any generation of entropy within a refrigeration or heat pump system increases the work requirement W˙ , and thus the operating cost. The extra work to overcome irreversibilities is TH S˙gen for a refrigerator and TLS˙gen for a heat pump. One will aim at reducing all causes for entropy generation, i.e., friction, heat transfer over finite temperature difference, etc., as much as possible.
The theoretical limit for the work of the refrigeration and heat pump systems are obtained for fully reversible engines, for which S˙gen = 0. This results in the expressions for a Carnot refrigerator and a Carnot heat pump, respectively, which read
Also the performance of refrigerators and heat pumps is measured by di- mensionless efficiency measures that compare the output (“what you get”) to the input (“what you pay for”), which here are the ratios of heat re- moved/supplied to the work required to run the device, known as the coef– ficients of performance (COP). We obtain, for refrigerator and heat pump operating between two reservoirs,
The COP of a refrigerator can be above or below unity, but the COP of a heat pump is never below unity. A resistance heater (RH), which converts electrical power W˙ RH fully into heat Q˙ RH = W˙ RH has a COP of unity, COPRH = 1, which is the lower bound for heat pumps. A typical heat pump has a COP above unity and gives more efficient heating.
Irreversible processes in engines lead to entropy generation and reduce the COP. For fully reversible engines we find the COP of Carnot engines,
The COPs for the Carnot refrigerator and Carnot heat pump are the max- imum possible COP for refrigeration or heat pump processes between two heat reservoirs at TH , TL.
Kelvin-Planck and Clausius Statements
Clausius’ statement of the second law says that heat will not go from cold to warm by itself. Note that the two words “by itself” are important here: a heat pump system can transfer heat from cold to warm, but work must be supplied, so the heat transfer is not “by itself.”
The Kelvin-Planck statement of the second law says that it is impossible to construct a device operating at steady state that receives heat from a single reservoir and produces work. In other words, no heat engine can be build that has a thermal efficiency of ηth = 1. In our treatment, this statement followed from the evaluation of the second law, while the Clausius statement was used explicitly in its development.
The Clausius statement is a daily experience—when we touch a hot plate, we do not expect to get colder hands—but the Kelvin-Planck statement might be more difficult to grasp. It is instructive to show that both statements are equivalent. To this end, we consider the setting shown in Fig. 5.5, consisting of an engine I that completely converts the heat Q˙ H to power ˙ = Q˙ H , and an engine II, a heat pump that consumes the work produced by engine I. Engine I is forbidden by the Kelvin-Planck statement while engine II is allowed by the Clausius statement. As the figure shows, the net effect of the
combined system [I + II] is heat transfer from cold to warm “by itself”, which is forbidden by the Clausius statement. Both statements are equivalent.